
如图,平面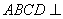 平面
平面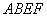 ,
,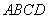 是正方形,
是正方形,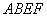 是矩形,且
是矩形,且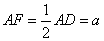 ,
,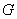 是
是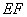 的中点,
的中点,
(Ⅰ) 求证:平面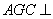 平面
平面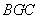 ;
;
(Ⅱ) 求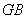 与平面
与平面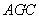 所成角的正弦值.
所成角的正弦值.
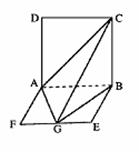
(Ⅰ) 证明:正方形ABCD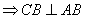 ∵面ABCD⊥面ABEF且交于AB,
∵面ABCD⊥面ABEF且交于AB,
 ∴CB⊥面ABEF ∵AG,GB
∴CB⊥面ABEF ∵AG,GB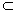 面ABEF, ∴CB⊥AG,CB⊥BG
面ABEF, ∴CB⊥AG,CB⊥BG
又AD=2a,AF= a,ABEF是矩形,G是EF的中点,
∴AG=BG=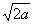 ,AB=2a, AB2=AG2+BG2,∴AG⊥BG
,AB=2a, AB2=AG2+BG2,∴AG⊥BG
∵CG∩BG=B
∴AG⊥平面CBG 而AG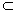 面AGC,
面AGC,
故平面AGC⊥平面BGC. …………………6分
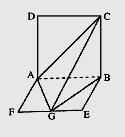
(Ⅱ) 解:如图,由(Ⅰ)知面AGC⊥面BGC,且交于GC,
在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,
∴∠BGH是GB与平面AGC所成的角.
∴在Rt△CBG中,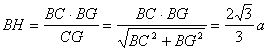 .
.
又BG=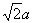 ,
,
∴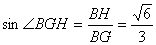 . …………………12分
. …………………12分


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
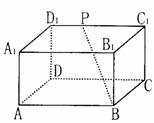
如图,长方体ABCD—A1B1C1D1中,BB1=BC,P为C1D1上一点,则异面直线PB与B1C所成角的大小( )
A.是45° B.是60°
C.是90° D.随P点的移动而变化
查看答案和解析>>
科目:高中数学 来源: 题型:
某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有( )种.
A.150 B.300 C.600 D.900
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com