
(1)a1=0,an+1=an+(2n-1)(n∈N*);
(2)a1=1,an+1=![]() (n∈N*).
(n∈N*).
科目:高中数学 来源: 题型:
|
| a11 | a12 | … | a1m |
| a21 | a22 | … | a2m |
| … | … | … | … |
| an1 | an2 | … | anm |
查看答案和解析>>
科目:高中数学 来源:2008届福建省厦门双十中学高三年级月考数学试题(理科)(含答案) 题型:044
对于某些正整数n,存在A1,A2,…,An为集合{1,2,……,n}的n个不同子集,满足下列条件:对任意不大于n的正整数i,j,①![]() 且每个Ai至少含有四个元素;②i∈Aj的充要条件是
且每个Ai至少含有四个元素;②i∈Aj的充要条件是![]() (其中i≠j).为了表示这些子集,作n行n列的数表,规定第i行第j列的数为
(其中i≠j).为了表示这些子集,作n行n列的数表,规定第i行第j列的数为
(1)求该数表中每列至多有多少个-1.
(2)用n表示该数表中1的个数,并证明n≥9
(3)请构造出集合{1,2,……,9}的9个不同子集A1,A2,…A9,使得A1,A2,…A9,满足题设(写出一种答案即可).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市西城区高三二模考试理科数学 题型:解答题
((本小题满分13分)
若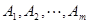 为集合
为集合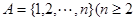 且
且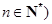 的子集,且满足两个条件:
的子集,且满足两个条件:
① ;
;
②对任意的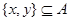 ,至少存在一个
,至少存在一个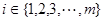 ,使
,使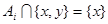 或
或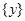 .
.
则称集合组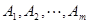 具有性质
具有性质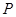 .
.
如图,作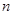 行
行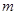 列数表,定义数表中的第
列数表,定义数表中的第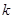 行第
行第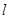 列的数为
列的数为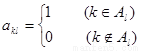 .
.
|
|
|
… |
|
|
|
|
… |
|
|
… |
… |
… |
… |
|
|
|
… |
|
(Ⅰ)当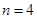 时,判断下列两个集合组是否具有性质
时,判断下列两个集合组是否具有性质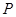 ,如果是请画出所对应的表格,如果不是请说明理由;
,如果是请画出所对应的表格,如果不是请说明理由;
集合组1: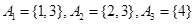 ;
;
集合组2: .
.
(Ⅱ)当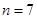 时,若集合组
时,若集合组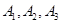 具有性质
具有性质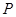 ,请先画出所对应的
,请先画出所对应的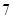 行3列的一个数表,再依此表格分别写出集合
行3列的一个数表,再依此表格分别写出集合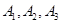 ;
;
(Ⅲ)当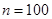 时,集合组
时,集合组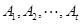 是具有性质
是具有性质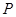 且所含集合个数最小的集合组,求
且所含集合个数最小的集合组,求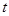 的值及
的值及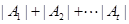 的最小值.(其中
的最小值.(其中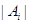 表示集合
表示集合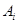 所含元素的个数)
所含元素的个数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com