
分析 (1)利用点A(4,m)在抛物线上,且|AF|=5,求出p,即可求出抛物线的标准方程;
(2)对“是否存在性”问题,先假设存在,设直线l的方程为x=k(y-1)(k≠0),与抛物线方程联立结合根的判别式求出k的范围,再利用向量垂直求出k值,看它们之间是否矛盾,没有矛盾就存在,否则不存在.
解答 解:(1)∵点A(4,m)在抛物线上,且|AF|=5,
∴4+$\frac{p}{2}$=5,
∴p=2,
∴抛物线的标准方程为y2=4x;
(2)由题可设直线l的方程为x=k(y-1)(k≠0),
代入抛物线方程得y2-4ky+4k=0;△=16k2-16k>0⇒k<0ork>1,
设B(x1,y1),C(x2,y2),则y1+y2=4k,y1y2=4k,
由$\overrightarrow{OB}$•$\overrightarrow{OC}$=0,即x1x2+y1y2=0⇒(k2+1)y1y2-k2(y1+y2)+k2=0,
解得k=-4或k=0(舍去),
∴直线l存在,其方程为x+4y-4=0.
点评 本小题主要考查曲线与方程,直线和抛物线等基础知识,以及求解存在性问题的基本技能和综合运用数学知识解决问题的能力.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|x<-2或x>1} | D. | {x|-2<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p:x∈R,x2-x-1<0,则¬p:x∈R,x2-x-1>0. | |
| B. | 命题:“若x2=1,则x=1或x=-1”的逆否命题是:“若x≠1且x≠-1,则x2≠1” | |
| C. | “$φ=\frac{π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 | |
| D. | 命题p:若$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,k2-2),则k=2是$\overrightarrow{a}⊥\overrightarrow{b}$的充分不必要条件;命题q:若幂函数f(x)=xa(a∈R)的图象过点(2,$\frac{\sqrt{2}}{2}$),则f(4)=$\frac{1}{2}$,则p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,ln2) | B. | (2,-ln2) | C. | (-ln2,2) | D. | (ln2,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥2 | B. | $\frac{1}{2}$≤a<1 | C. | $\frac{1}{2}$<a<1 | D. | a≥2或$\frac{1}{2}$≤a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
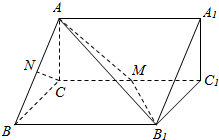 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com