
已知函数 ,其中
,其中 是自然对数的底数,
是自然对数的底数, .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,求函数
时,求函数 的最小值.
的最小值.
(Ⅰ) 的单调减区间为
的单调减区间为 ;单调增区间为
;单调增区间为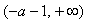 ;(Ⅱ)
;(Ⅱ)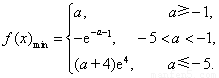
【解析】
试题分析:(Ⅰ)先求导函数,得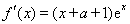 ,令
,令 ,得递增区间为
,得递增区间为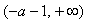 ;令
;令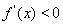 ,得递减区间为
,得递减区间为 ;(Ⅱ)令
;(Ⅱ)令 ,得
,得 ,讨论
,讨论 与区间
与区间 的位置关系,当
的位置关系,当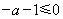 ,或
,或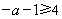 时,函数单调,利用单调性求最值;当
时,函数单调,利用单调性求最值;当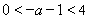 ,将定义域分段,分别判断导函数符号,得单调区间,判断函数的值图像,从而求得最值.
,将定义域分段,分别判断导函数符号,得单调区间,判断函数的值图像,从而求得最值.
试题解析:(Ⅰ)解:因为 ,
, ,所以
,所以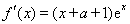 .
.
令 ,得
,得 .当
.当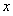 变化时,
变化时, 和
和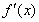 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
故 的单调减区间为
的单调减区间为 ;单调增区间为
;单调增区间为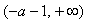 .
.
(Ⅱ)解:由(Ⅰ),得 的单调减区间为
的单调减区间为 ;单调增区间为
;单调增区间为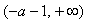 .
.
所以当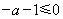 ,即
,即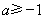 时,
时, 在
在 上单调递增,
上单调递增,
故 在
在 上的最小值为
上的最小值为 ;
;
当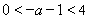 ,即
,即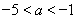 时,
时,
 在
在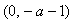 上单调递减,
上单调递减,  在
在 上单调递增,
上单调递增,
故 在
在 上的最小值为
上的最小值为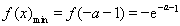 ;
;
当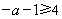 ,即
,即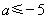 时,
时, 在
在 上单调递减,
上单调递减,
故 在
在 上的最小值为
上的最小值为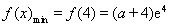 .
.
所以函数 在
在 上的最小值为
上的最小值为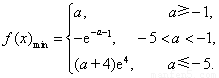
考点:1、导数在单调性上的应用;2、导数在极值、最值上的应用.


科目:高中数学 来源: 题型:
(本小题满分14分)已知函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数,![]() 为正数)
为正数)
(I)若![]() 在
在![]()
![]() 处取得极值,且
处取得极值,且![]() 是
是![]() 的一个零点,求
的一个零点,求![]() 的值;(II)若
的值;(II)若![]() ,求
,求![]() 在区间
在区间![]() 上的最大值;(III)设函数
上的最大值;(III)设函数![]() 在区间
在区间![]() 上是减函数,求
上是减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东华附、省高三上学期期末联考理数学卷(解析版) 题型:解答题
已知函数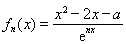 ,其中
,其中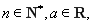
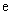 是自然对数的底数.
是自然对数的底数.
(1)求函数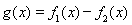 的零点;
的零点;
(2)若对任意
 均有两个极值点,一个在区间
均有两个极值点,一个在区间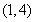 内,另一个在区间
内,另一个在区间 外,
外,
求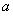 的取值范围;
的取值范围;
(3)已知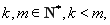 且函数
且函数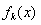 在
在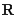 上是单调函数,探究函数
上是单调函数,探究函数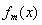 的单调性.
的单调性.
查看答案和解析>>
科目:高中数学 来源:2014届河北省高三上学期一调考试文科数学试卷(解析版) 题型:解答题
已知函数 ,其中
,其中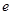 是自然对数的底数,
是自然对数的底数,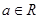 .
.
(1)若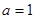 ,求曲线
,求曲线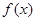 在点
在点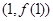 处的切线方程;
处的切线方程;
(2)若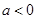 ,求
,求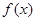 的单调区间;
的单调区间;
(3)若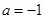 ,函数
,函数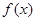 的图象与函数
的图象与函数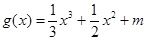 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数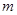 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届河北省石家庄市高二下学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数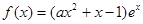 ,其中
,其中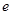 是自然对数的底数,
是自然对数的底数,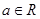 .
.
(1)若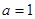 ,求曲线
,求曲线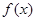 在点
在点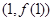 处的切线方程;
处的切线方程;
(2)若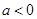 ,求
,求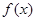 的单调区间;
的单调区间;
(3)若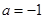 ,函数
,函数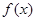 的图象与函数
的图象与函数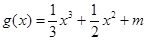 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com