
(2005
全国Ⅲ,18)如下图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(1)
证明:AB⊥平面VAD;(2)
求面VAD与面VDB所成的二面角的大小.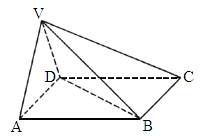
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:044
(2005
全国Ⅱ,22)已知a≥0,函数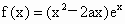 .
.
(1)
当x为何值时,f(x)取得最小值?证明你的结论;(2)
设f(x)在[-1,1]上是单调函数,求a的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:022
(2005
全国Ⅲ,15)设l为平面上过点(0,1)的直线,l的斜率等可能地取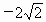 ,
,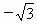 ,
,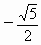 ,0,
,0,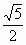 ,
,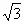 ,
,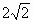 .用ξ表示坐标原点到l的距离,则随机变量ξ数学期望Eξ=________.
.用ξ表示坐标原点到l的距离,则随机变量ξ数学期望Eξ=________.查看答案和解析>>
科目:高中数学 来源: 题型:044
(2005
全国I,20)9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为0.5.若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没有发芽,则这个坑需要补种.假定每个坑至多补种一次,每次种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望(精确到0.01).查看答案和解析>>
科目:高中数学 来源: 题型:
【练】
(1)(2005全国卷1)已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,![]() 与
与![]() 共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且
共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且![]() ,证明
,证明![]() 为定值。
为定值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com