
(2006
福州模拟)如下图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,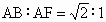 ,M为线段EF的中点.
,M为线段EF的中点.
(1)
求证:AM⊥平面BDF;(2)
求二面角A-DF-B的大小.
|
解析: (1)设AC∩BD=O,连结OM,
因为 ABCD为正方形,所以AC⊥BD,又平面 ABCD⊥平面ACEF,且平面ABCD∩平面ACEF=AC,则 BD⊥平面ACEF,所以BD⊥AM.又因为 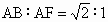 ,而 ,而 , ,
所以 AF=AO,∵ M为矩形ACEF的边EF的中点,∴四边形 OAFM为正方形,∴AM⊥OF.∵ BD∩OF=O,且OF、BD 平面BDF, 平面BDF,
∴ AM⊥平面BDF.(2) 因为平面ABCD⊥平面ACEF,且平面ABCD∩平面ACEF=AC,而 ACEF为矩形,即AF⊥AC,所以 AF⊥平面ABCD,得AB⊥AF,又 ABCD为正方形,则AB⊥AD,∵ AD∩AF=A,∴AB⊥平面ADF.在平面 ADF内过A作AG⊥DF于点G,连BG,则由三垂线定理知BG⊥DF,所以∠ AGB即为二面角A-DF-B的平面角.设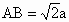 ,AF=a(a>0),则 ,AF=a(a>0),则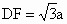 ,所以 ,所以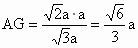 .则在Rt△ABG中, .则在Rt△ABG中, ,所以∠AGB=60°,即二面角A-DF-B的大小为60°. ,所以∠AGB=60°,即二面角A-DF-B的大小为60°. |


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com