
(2006
天津,22)如下图,以椭圆 (a>b>0)的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连结OA交小圆于点B.设直线BF是小圆的切线.
(a>b>0)的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连结OA交小圆于点B.设直线BF是小圆的切线.
(1)
证明 ,并求直线BF与y轴的交点M的坐标;
,并求直线BF与y轴的交点M的坐标;
(2)
设直线BF交椭圆于P、Q两点,证明 .
.

|
证明: (1)由题设条件,知Rt△OFA~Rt△OBF,故  ,即 ,即 .因此, .因此, . ① . ①
在 Rt△OFA中, . .
于是,直线 OA的斜率 .设直线BF的斜率为k, .设直线BF的斜率为k,
则  .这时,直线BF的方程为 .这时,直线BF的方程为 , ,
令 x=0,则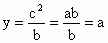 .所以直线BF与y轴的交点为M(0,a). .所以直线BF与y轴的交点为M(0,a).
(2) 由(1)得直线BF的方程为y=kx+a,且  . ② . ②
由已知,设 P(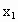 , , )、Q( )、Q(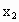 , ,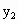 ),则它们的坐标满足方程组 ),则它们的坐标满足方程组
由方程组③消去 y,并整理得
由式①、②和④,  . .
由方程组③消去 x,并整理得
由式②和⑤,
综上,得到
注意到  ,得 ,得
|
|
剖析:本小题主要考查椭圆的标准方程和几何性质、直线方程、平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com