
定义在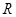 上的函数
上的函数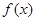 同时满足性质:①对任何
同时满足性质:①对任何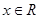 ,均有
,均有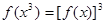 成立;②对任何
成立;②对任何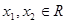 ,当且仅当
,当且仅当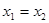 时,有
时,有 .则
.则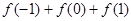 的值为 .
的值为 .
0
【解析】
试题分析:首先根据题干条件解得f(0),f(-1)和f(-1)的值,然后根据对任何x1,x2∈R,x1≠x2均有f(x1)≠f(x2)可以判断f(0)、f(-1)和f(1)不能相等,据此解得答案解:∵对任何x∈R均有f(x3)=[f(x)]3,∴f(0)=(f(0))3,解得f(0)=0,1或-1, f(-1)=(f(-1))3,解得f(-1)=0,1或-1, f(1)=(f(1))3,解得f(1)=0,1或-1,∵对任何x1,x2∈R,x1≠x2均有f(x1)≠f(x2),∴f(0)、f(-1)和f(1)的值只能是0、-1和1中的一个,∴f(0)+f(-1)+f(1)=0,故答案为0
考点:函数的值
点评:本题主要考查函数的值的知识点,解答本题的关键是根据题干条件判断f(0)、f(-1)和f(1)不能相等,本题很容易出错


科目:高中数学 来源: 题型:
定义在![]() 上的函数
上的函数![]() 同时满足以下条件:
同时满足以下条件:
①![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;②
上是增函数;②![]() 是偶函数;
是偶函数;
③![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,求函数
,求函数![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年辽宁省五校协作体高三上学期期中考试理科数学试卷(解析版) 题型:解答题
定义在 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数;
② 是偶函数;
是偶函数;
③ 在x=0处的切线与直线
在x=0处的切线与直线 y=x+2垂直.
y=x+2垂直.
(1)求函数 =
= 的解析式;
的解析式;
(2)设g(x)= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三第一次月考文科数学试卷(解析版) 题型:填空题
(本小题满分14分)
定义在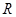 上的函数
上的函数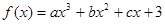 同时满足以下条件:
同时满足以下条件:
①  在
在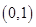 上是减函数,在
上是减函数,在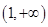 上是增函数;
②
上是增函数;
② 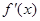 是偶函数;
是偶函数;
③  在
在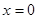 处的切线与直线
处的切线与直线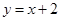 垂直.
垂直.
(1)求函数 的解析式;
的解析式;
(2)设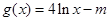 ,若存在
,若存在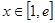 ,使
,使 ,求实数
,求实数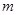 的取值范围.[
的取值范围.[
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省莱芜市高三4月自主检测文科数学试卷(解析版) 题型:解答题
定义在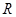 上的函数
上的函数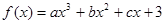 同时满足以下条件:
同时满足以下条件:
① 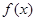 在
在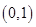 上是减函数,在
上是减函数,在 上是增函数;
②
上是增函数;
② 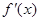 是偶函数;
是偶函数;
③ 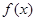 在
在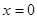 处的切线与直线
处的切线与直线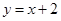 垂直.
垂直.
(1)求函数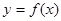 的解析式;
的解析式;
(2)设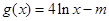 ,若存在
,若存在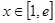 ,使
,使 ,求实数
,求实数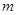 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省淄博市高三第一学期期末数学理卷 题型:解答题
(本小题满分12分) 定义在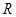 上的函数
上的函数 同时满足以下条件:①
同时满足以下条件:① 在
在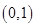 上是减函数,在
上是减函数,在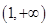 上是增函数;②
上是增函数;②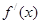 是偶函数;
是偶函数;
③ 在
在 处的切线与直线
处的切线与直线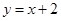 垂直.
垂直.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设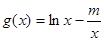 ,若存在
,若存在 ,使
,使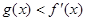 ,求实数
,求实数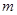 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com