
已知椭圆 的中心为直角坐标系
的中心为直角坐标系 的原点,焦点在
的原点,焦点在 轴上,它的一个顶点到两个焦点的距离分别是7和1。
轴上,它的一个顶点到两个焦点的距离分别是7和1。
(1)求椭圆 的方程;
的方程;
(2)若 为椭圆
为椭圆 上的动点,
上的动点, 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点, ,求点
,求点 的轨迹方程,并说明轨迹表示什么曲线。
的轨迹方程,并说明轨迹表示什么曲线。
(Ⅰ)设椭圆长半轴长及半焦距分别为 ,由已知得
,由已知得
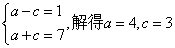 , ---------------2分
, ---------------2分
所以椭圆 的标准方程为
的标准方程为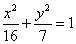 ---------------4分
---------------4分
(Ⅱ)设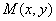 ,其中
,其中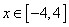 。由已知
。由已知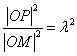 及点
及点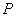 在椭圆
在椭圆 上可得
上可得
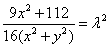 。
。
整理得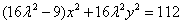 ,其中
,其中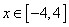 。---------------8分
。---------------8分
(i)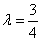 时。化简得
时。化简得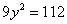
所以点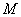 的轨迹方程为
的轨迹方程为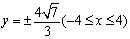 ,轨迹是两条平行于
,轨迹是两条平行于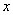 轴的线段。---------------10分
轴的线段。---------------10分
(ii)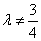 时,方程变形为
时,方程变形为 ,其中
,其中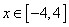
当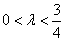 时,点
时,点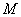 的轨迹为中心在原点、实轴在
的轨迹为中心在原点、实轴在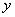 轴上的双曲线满足
轴上的双曲线满足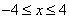
的部分。---------------13分
当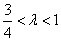 时,点
时,点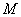 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在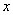 轴上的椭圆满足
轴上的椭圆满足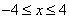 的部分;
的部分;
当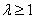 时,点
时,点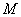 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在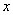 轴上的椭圆
轴上的椭圆
---------------16分
说明:没有考虑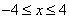 的至少要扣5分
的至少要扣5分


科目:高中数学 来源: 题型:
已知椭圆![]() 的中心为直角坐标系
的中心为直角坐标系![]() 的原点,焦点在
的原点,焦点在![]() 轴上,它的一个顶点到两个
轴上,它的一个顶点到两个
焦点的距离分别是7和1
(1)求椭圆![]() 的方程‘
的方程‘
(2)若![]() 为椭圆
为椭圆![]() 的动点,
的动点,![]() 为过
为过![]() 且垂直于
且垂直于![]() 轴的直线上的点,
轴的直线上的点,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 的中心为直角坐标系
的中心为直角坐标系![]() 的原点,焦点在
的原点,焦点在![]() 轴上,它的一个项点到两个焦点的距离分别是7和1
轴上,它的一个项点到两个焦点的距离分别是7和1
(1)求椭圆![]() 的方程‘
的方程‘
(2)若![]() 为椭圆
为椭圆![]() 的动点,
的动点,![]() 为过
为过![]() 且垂直于
且垂直于![]() 轴的直线上的点,
轴的直线上的点,![]()
(e为椭圆C的离心率),求点![]() 的轨迹方程,并说明轨迹是什么曲线。
的轨迹方程,并说明轨迹是什么曲线。
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)已知椭圆![]() 的中心为直角坐标系
的中心为直角坐标系![]() 的原点,焦点在
的原点,焦点在![]() 轴上,它的一个项点到两个焦点的距离分别是7和1.
轴上,它的一个项点到两个焦点的距离分别是7和1.
(I)求椭圆![]() 的方程;
的方程;
(II)若![]() 为椭圆
为椭圆![]() 的动点,
的动点,![]() 为过
为过![]() 且垂直于
且垂直于![]() 轴的直线上的点,
轴的直线上的点,![]() (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点![]() 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源:2015届河北衡水中学高二上第四次调研考试文数学卷(解析版) 题型:解答题
已知椭圆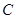 的中心为直角坐标系
的中心为直角坐标系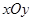 的原点,焦点在
的原点,焦点在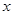 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆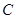 的方程;
的方程;
(2)若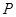 为椭圆
为椭圆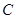 的动点,
的动点,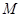 为过
为过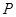 且垂直于
且垂直于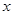 轴的直线上的点,
轴的直线上的点,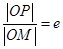 (
(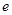 为椭圆的离心率),求点
为椭圆的离心率),求点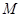 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源:2014届陕西省西安市高二上学期期末考试理科数学卷(解析版) 题型:解答题
已知椭圆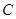 的中心为直角坐标系
的中心为直角坐标系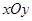 的原点,焦点在
的原点,焦点在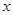 轴上,它的一个顶点到两个焦点的距离分别是7和1
轴上,它的一个顶点到两个焦点的距离分别是7和1
(1)求椭圆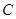 的方程
的方程
(2)若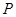 为椭圆
为椭圆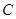 的动点,
的动点,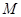 为过
为过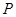 且垂直于
且垂直于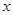 轴的直线上的点,
轴的直线上的点, (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点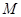 的轨迹方程,并说明轨迹是什么曲线?
的轨迹方程,并说明轨迹是什么曲线?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com