分析:设已知方程的左边为y1,右边为y2,故y2表示圆心为原点,半径为2的半圆,y2表示恒过定点(0,2)的直线,画出两函数的图象,如图所示,则原方程要只有一个实数根,即要半圆与直线只有一个公共点,根据图象可知当直线与半圆相切时满足题意,求出此时k的值,再求出两个特殊位置,直线再过(2,0),求出此时k的值,当k小于求出的值时满足题意,同时求出直线过(-2,0)时k的值,当k大于求出的值时满足题意,综上,得到所有满足题意的k的范围.
解答: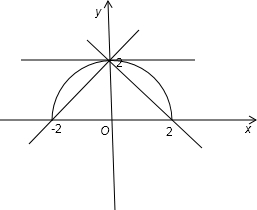
解:设y
1=
,y
2=kx+2,
则y
1表示圆心为原点,半径为2的x轴上方的半圆,y
2表示恒过(0,2)的直线,
画出两函数图象,如图所示,根据图象可得:
当直线与半圆相切,即直线为y=2时,直线与半圆只有一个公共点,
即方程
=kx+2只有一个实数根,此时k=0;
当直线过(0,2)和(2,0)时,直线的斜率为-1,
则当k<-1时,直线与半圆只有一个公共点,
即方程
=kx+2只有一个实数根;
当直线过(0,2)和(-2,0)时,直线的斜率为1,
则当k>1时,直线与半圆只有一个公共点,
即方程
=kx+2只有一个实数根,
综上,满足题意的k的范围是k=0或k>1或k<-1.
故答案为:k=0或k>1或k<-1
点评:此题考查了直线与圆相交的性质,以及函数的图象,考查了数形结合的思想,解此类题的思路为:把方程两边分别设为函数,借助图形,利用两函数图象的交点个数判断方程解的情况来解决问题,同时要求学生考虑问题要全面.

 解:设y1=
解:设y1=

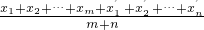 的值为
的值为

 的值为( )
的值为( )

 的值为( )
的值为( )
