
用总长为14.8米的钢条制成一个长方体容器的框架,如果所制的容器的底面的长比宽多0.5米,那么高为多少时容器的容器最大?并求出它的最大容积.
容器高为1.2m时容器的容积最大,最大容积为1.8m3.
【解析】
试题分析:令容器底面宽为 m, 则长为(x+0.5)m,高为(3.2-2x)m,由实际意义可得0<x<1.6,由长方体体积写出容积
m, 则长为(x+0.5)m,高为(3.2-2x)m,由实际意义可得0<x<1.6,由长方体体积写出容积 的表达式
的表达式 ,求导得
,求导得 ,进而求得0<x<1时,
,进而求得0<x<1时, ;1<x<1.6时,
;1<x<1.6时, ,可知当
,可知当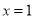 时
时 有最大值,求之得最大容积.
有最大值,求之得最大容积.
【解析】
设容器底面宽为x m,则长为(x+0.5)m,高为(3.2-2x)m,
由 解得0<x<1.6, 3分
解得0<x<1.6, 3分
设容器的容积为y ,
,
则有y=x(x+0.5)(3.2-2x)= 6分
6分
 ,
,
令 =0,即
=0,即 ,
,
解得x=1,或x= (舍去). 8分
(舍去). 8分
∵0<x<1时, ;1<x<1.6时,
;1<x<1.6时, ,
,
∴在定义域(0,1.6)内x=1是唯一的极值点,且是极大值点,
∴当x=1时,y取得最大值为1.8, 10分
此时容器的高为3.2-2=1.2m,
因此,容器高为1.2m时容器的容积最大,最大容积为1.8 . 12分
. 12分
考点:利用导数求函数的最值,函数的应用.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中理科数学试卷(解析版) 题型:选择题
复数z满足z(2+i)=2i-1,则复数z的实部与虚部之和为
A、1 B、-1 C、2 D、3
查看答案和解析>>
科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试理科数学试卷(解析版) 题型:选择题
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)( ).

A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com