
数列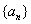 中,
中, ,
,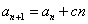 (
(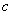 是常数,
是常数,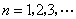 ),且
),且 成公比不为
成公比不为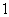 的等比数列,则
的等比数列,则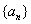 的通项公式是 .
的通项公式是 .
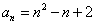
【解析】
试题分析:a1=2,a2=2+c,a3=2+3c,因为a1,a2,a3成等比数列,所以(2+c)2=2(2+3c),解得c=0或c=2.当c=0时,a1=a2=a3,不符合题意舍去,故c=2.当n≥2时,由于a2-a1=c,a3-a2=2c,an-an-1=(n-1)c,所以an-a1=[1+2++(n-1)]c=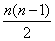 c.又a1=2,c=2,故an=2+n(n-1)=n2-n+2(n=2,3,).当n=1时,上式也成立,所以an=n2-n+2
c.又a1=2,c=2,故an=2+n(n-1)=n2-n+2(n=2,3,).当n=1时,上式也成立,所以an=n2-n+2
考点:本题考查了数列的性质和应用
点评:掌握常见数列通项公式的求法如叠加法、叠乘法是解决此类问题的关键,解题时要注意计算能力的培养.


科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(北京) 题型:解答题
(本小题共13分)数列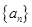 中,
中,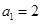 ,
,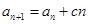 (
(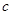 是常数,
是常数,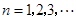 ),且
),且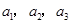 成公比不为
成公比不为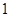 的等比数列.
的等比数列.
(I)求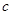 的值;
的值;
(II)求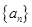 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省高三第七次适应性训练文科数学试卷(解析版) 题型:解答题
数列 中,
中,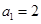 ,
,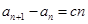 (
(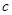 是常数,
是常数,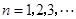 ),且
),且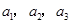 成公比不为
成公比不为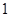 的等比数列.
的等比数列.
(Ⅰ)求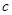 的值;
的值;
(Ⅱ)求 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com