Question

已知椭圆上一点M(1，)，P、Q是椭圆上异于M的两个动点．

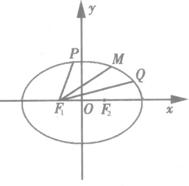
(1)若P、M、Q到椭圆左焦点F₁的距离成等差数列，求证：线段PQ的垂直平分线经过一个定点A；

(2)若PQ为过左焦点F₁且与两轴都不垂直的弦，在x轴上求一点N，使NF₁为∠PNQ的平分线．

Answer 1

解:(1)设P(x₁,y₁),O(x₂,y₂),椭圆中a=2,b=,c=,e=.

∵|PF₁|=2+x₁,|MF₁|=2+,|QF₁|=2+x₂,依题意,2|MF₁|=|PF₁|+|QF₁|,

∴x₁+x₂=2,设PQ中点为C(x₀,y₀),

线段PQ的垂直平分线为l,则

x₀=,

∵

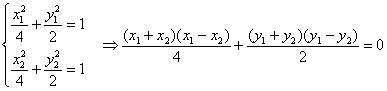
+y₀(y₁-y₂)=0

∵y₀≠0,∴k_PQ=,∵PQ⊥l,∴k_l=2y₀,

∴l的方程是y-y₀=2y₀(x-1),即

y=y₀(2x-1),∴直线过定点(,0).

(2)设N(x₀,0),PQ的方程为x=my-代入中整理得:

(m²+2)y²-2my-2=0,设P(x₁,y₁),Q(x₂,y₂),则

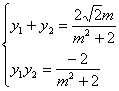
又NF₁为∠PNQ的平分线,∴K_NP+K_NQ=0

即,

y₁(x₂-x₀)+y₂(x₁-x₀)=0,y₁x₂+y2x₁-x₀(y₁+y₂)=0,

y₁(my₂-)+y₂(my₁-)-x₀(y₁+y₂)=0,

2m()-(x₀+)=0,

∴x₀=-2,故N(-2,0).