
关于下列命题:①函数 在第一象限是增函数;②函数
在第一象限是增函数;②函数 是偶函数; ③函数
是偶函数; ③函数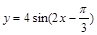 的一个对称中心是(
的一个对称中心是(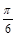 ,0);④函数
,0);④函数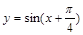 在闭区间
在闭区间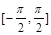 上是增函数; 写出所有正确的命题的题号: 。
上是增函数; 写出所有正确的命题的题号: 。
③
解析试题分析:利用正切函数单调性判断①的正误;利用余弦函数的奇偶性判断②的正误;把对称中心坐标代入方程,是否处理确定③的正误;利用函数的单调性判断④的正误。
解:①函数y=tanx在第一象限是增函数;显然不正确,正切函数在类似[0,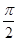 )上是增函数,第一象限是增函数,错误.②函数
)上是增函数,第一象限是增函数,错误.②函数 =sin2x是偶函数,是错误的;③因为x=
=sin2x是偶函数,是错误的;③因为x=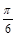 时,函数y=4sin(2x-
时,函数y=4sin(2x-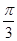 )=0,所以函数y=4sin(2x-
)=0,所以函数y=4sin(2x-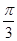 )的一个对称中心是(
)的一个对称中心是(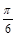 ,0);正确.④函数
,0);正确.④函数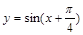 )在闭区间[-
)在闭区间[-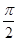 ,
,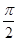 ]上是增函数.这是不正确的.在[-
]上是增函数.这是不正确的.在[-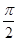 ,
,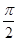 ]上函数有增有减.故答案为:③
]上函数有增有减.故答案为:③
考点:三角函数的基本性质
点评:本题是基础题,考查三角函数的基本性质,包括:对称性、奇偶性、单调性、对称中心的知识,明确基本函数的基本性质,是解题的关键,所以平时学习注意基本知识的掌握和巩固


科目:高中数学 来源: 题型:填空题
下面有五个命题:
①函数 的最小正周期是
的最小正周期是
②终边在y轴上的角的集合是{ }
}
③在同一坐标系中,函数 的图象和函数y=x的图象有三个公共点
的图象和函数y=x的图象有三个公共点
④把函数 的图象向右平移
的图象向右平移 得到
得到 的图象
的图象
⑤函数 上是减函数
上是减函数
其中,真命题的编号是 (写出所有真命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com