
已知函数f(x)=x3+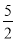 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+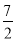 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(1)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(2)设函数f(x)的导函数为f’(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
(1)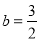 ;(2)
;(2)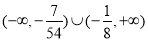 ;(3)
;(3)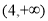
【解析】
试题分析:(1)根据导数的几何意义,先求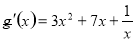 ,利用
,利用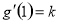 ,然后将
,然后将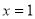 代入,求出`
代入,求出`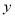 ,此点也在函数f(x)上,代入,即可求出
,此点也在函数f(x)上,代入,即可求出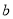 ;
;
(2)根据 ,消去
,消去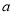 ,得到关于
,得到关于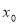 的三次方程,,此方程有唯一解,令
的三次方程,,此方程有唯一解,令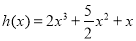 ,求出
,求出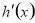 ,利用导数求出极值点,以及两侧的单调性,从而分析图像,得到
,利用导数求出极值点,以及两侧的单调性,从而分析图像,得到 的取值范围;
的取值范围;
(3)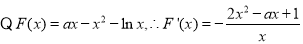 ,因为存在极值,所以
,因为存在极值,所以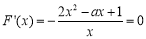 在
在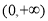 上有根即方程
上有根即方程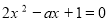 在
在 上有根.得到根与系数的关系,代入极值
上有根.得到根与系数的关系,代入极值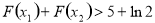 ,得到
,得到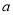 的取值范围.
的取值范围.
试题解析:(1)∵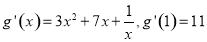 所以直线
所以直线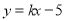 的
的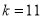 ,当
,当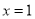 时,
时,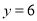 ,将(1,6)代入
,将(1,6)代入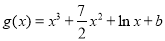 ,得
,得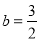 . 4分
. 4分
(2)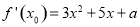 ,由题意知
,由题意知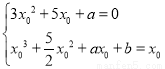 消去
消去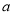 ,
,
得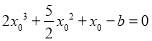 有唯一解.
有唯一解.
令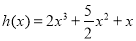 ,则
,则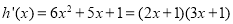 , 6分
, 6分
所以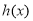 在区间上是增函数,在
在区间上是增函数,在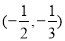 上是减函数,
上是减函数,
又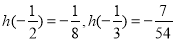 ,故实数
,故实数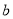 的取值范围是
的取值范围是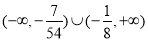 . 9分
. 9分
(3)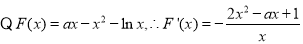
因为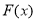 存在极值,所以
存在极值,所以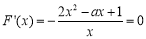 在
在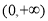 上有根即方程
上有根即方程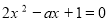 在
在 上有根. 10分
上有根. 10分
记方程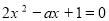 的两根为
的两根为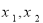 由韦达定理
由韦达定理 ,所以方程的根必为两不等正根. 12分
,所以方程的根必为两不等正根. 12分
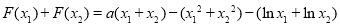

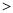
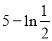 所以
所以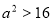 满足方程
满足方程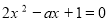 判别式大于零
判别式大于零
故所求取值范围为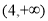 14分
14分
考点:1.导数的几何意义;2.利用导数求函数极值,单调性;3.导数解决函数的综合问题.


科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考文科数学试卷(解析版) 题型:选择题
给出下列命题,其中真命题的个数是( )
①存在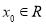 ,使得
,使得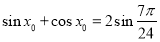 成立;
成立;
②对于任意的三个平面向量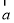 、
、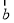 、
、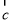 ,总有
,总有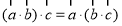 成立;
成立;
③相关系数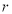 (
(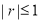 ),
),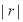 值越大,变量之间的线性相关程度越高.
值越大,变量之间的线性相关程度越高.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟理科数学试卷(解析版) 题型:选择题
双曲线 =1(a>0,b>0)的右焦点是抛物线y2=8x的焦点F,两曲线的一个公共点为P,且|PF| =5,则此双曲线的离心率为( )
=1(a>0,b>0)的右焦点是抛物线y2=8x的焦点F,两曲线的一个公共点为P,且|PF| =5,则此双曲线的离心率为( )
A.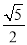 B.
B.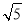 C.2 D.
C.2 D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟文科数学试卷(解析版) 题型:解答题
在△ABC中,a、b、c分别为角A、B、C所对的边,且
(2b+c)cosA+acosC =0
(1)求角A的大小:
(2)求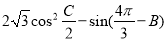 的最大值,并求取得最大值时角 B.C的大小.
的最大值,并求取得最大值时角 B.C的大小.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟文科数学试卷(解析版) 题型:选择题
已知角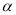 的顶点与原点重合,始边与x轴的非负半轴重合,终边过点
的顶点与原点重合,始边与x轴的非负半轴重合,终边过点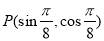 ,则sin(2
,则sin(2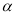 -
-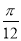 )=( )
)=( )
A.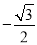 B.
B.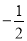 C.
C.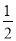 D.
D.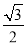
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
实验员进行一项实验,先后要实施5个程序,其中程序A只能出现在第一步或最后一步,程序C或D实施时必须相邻,实验顺序的编排方法共有________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com