
已知函数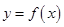 和
和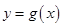 的图象关于
的图象关于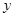 轴对称,且
轴对称,且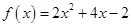 .
.
(1)求函数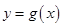 的解析式;
的解析式;
(2)当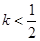 时,解不等式
时,解不等式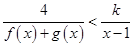 .
.
(1)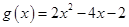 ;(2)当
;(2)当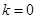 ,解集为
,解集为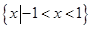 ;
;
当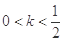 ,解集为
,解集为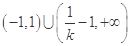 ;当
;当 ,解集为
,解集为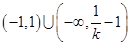 .
.
【解析】
试题分析:(1)先利用两个函数图象关于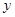 轴对称的关系,得出函数
轴对称的关系,得出函数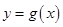 上的点
上的点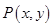 与其关于
与其关于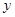 轴对称点
轴对称点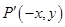 在函数
在函数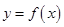 ,进而通过坐标之间的关系得出函数
,进而通过坐标之间的关系得出函数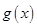 的解析式;(2)先将不的公式进行等价变形,得到
的解析式;(2)先将不的公式进行等价变形,得到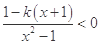 ,等价转化为
,等价转化为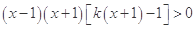 ,就
,就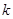 的取值进行分类讨论,主要是对
的取值进行分类讨论,主要是对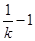 与
与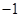 和
和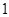 的大小进行分类讨论,从而确定不等式的解集.
的大小进行分类讨论,从而确定不等式的解集.
试题解析:(1)设函数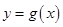 图象上任意一点
图象上任意一点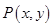 ,
,
由已知点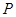 关于
关于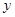 轴对称点
轴对称点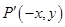 一定在函数
一定在函数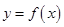 图象上,
图象上,
代入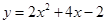 ,得
,得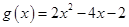 ;
;
(2)由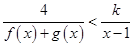 整理得不等式为
整理得不等式为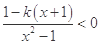 ,
,
等价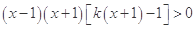 ,
,
当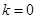 ,不等式为
,不等式为 ,解为
,解为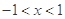 .
.
当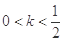 ,整理为
,整理为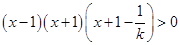 ,解为
,解为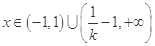 .
.
当 ,不等式整理为
,不等式整理为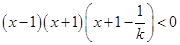 ,解为
,解为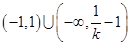 .
.
综上所述,当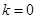 ,解集为
,解集为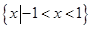 ;
;
当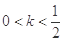 ,解集为
,解集为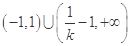 ;
;
当 ,解集为
,解集为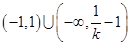 .
.
考点:1.函数图象的对称性;2.利用分类讨论法求解含参不等式


科目:高中数学 来源:2014届广东省、阳东一中高二上联考文数试卷(解析版) 题型:解答题
(本题满分14分)
已知函数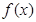 和
和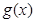 的图象关于原点对称,且
的图象关于原点对称,且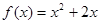 .
.
(1)求函数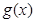 的解析式;
的解析式;
(2)若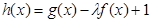 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数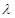 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省石家庄市高三数学练习试卷4 题型:解答题
(本小题满分14分)
已知函数 和
和 的图象关于原点对称,且
的图象关于原点对称,且 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)解不等式 ;
;
(Ⅲ)若 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com