
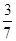 ,
,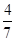 .
.科目:高中数学 来源:不详 题型:解答题
 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:| 分组 |  组 组 |  组 组 |  组 组 |
| 药品有效 |  |  |  |
| 药品无效 |  |  |  |
 个,抽到
个,抽到 组药品有效的概率是
组药品有效的概率是 .
. 个测试结果,问应在
个测试结果,问应在 组抽取样本多少个?
组抽取样本多少个?  ,
, ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于 %,则认为测试通过).
%,则认为测试通过).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
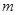 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为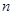 ,求
,求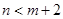 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,取到黑球或黄球的概率是
,取到黑球或黄球的概率是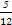 ,取到黄球或绿球的概率也是
,取到黄球或绿球的概率也是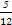 ,则取到黑球、黄球、绿球的概率分别是 .
,则取到黑球、黄球、绿球的概率分别是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ( )
( )A.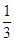 | B.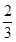 | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
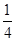 ,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=
,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=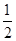 ,则随机变量X的数学期望为________.
,则随机变量X的数学期望为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
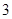 位教师安排在周一至周五中的
位教师安排在周一至周五中的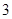 天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )
天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )A.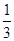 | B.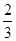 | C.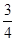 | D.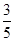 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com