
| A. | $\frac{7}{25}$ | B. | $-\frac{7}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |
分析 由已知利用同角三角函数基本关系式可求cosα=$\frac{3}{5}$,sinα=$\frac{4}{5}$,cosβ=$\sqrt{1-si{n}^{2}β}$,代入两角差的余弦函数公式化简可求sinβ的值.
解答 解:∵0<a<$\frac{π}{2},-\frac{π}{2}<β<0,cos({α-β})=-\frac{3}{5}$,tanα=$\frac{4}{3}$,
∴cosα=$\sqrt{\frac{1}{1+ta{n}^{2}α}}$=$\frac{3}{5}$,sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{4}{5}$,cosβ=$\sqrt{1-si{n}^{2}β}$,
∴由cosαcosβ+sinαsinβ=-$\frac{3}{5}$,可得:$\frac{3}{5}$$\sqrt{1-si{n}^{2}β}$+$\frac{4}{5}$sinβ=-$\frac{3}{5}$,
∴整理可得:25sin2β+24sinβ=0,
∴解得:sinβ=-$\frac{24}{25}$,或0(舍去).
故选:D.
点评 本题主要考查了同角三角函数基本关系式,两角差的余弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
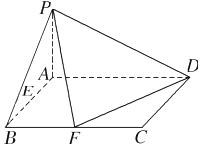 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| T(分钟) | 25 | 30 | 35 | 40 |
| 频数(次) | 100 | 150 | 200 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com