
已知函数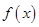 是R上的奇函数,若对于
是R上的奇函数,若对于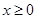 ,都有
,都有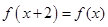 ,
, 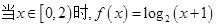 时,
时,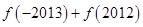 的值为
的值为
A.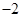 | B.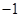 | C.1 | D.2 |
B
解析试题分析:根据函数的奇偶性可得f(-2013)=-f(2013),根据函数的周期性可得f(2012)=f(0),f(2013)=f(1),结合x∈[0,2)时,f(x)=log2(x+1),代入可得答案.解:∵函数f(x)是定义在R上的奇函数,∴f(-2013)=-f(2013),又∵x≥0,都有f(x+2)=f(x),,故f(2012)=f(0),f(2013)=f(1),又由当x∈[0,2)时,f(x)=log2(x+1),,∴f(2012)+f(-2013)=f(2012)-f(2013)=f(0)-f(1)=log21-log22=0-1=-1,故选C
考点:对数函数图象与性质
点评:本题考查的知识点是对数函数图象与性质的综合应用,函数奇偶性的性质,其中熟练掌握函数的奇偶性和周期性是解答的关键


科目:高中数学 来源: 题型:单选题
下列各组函数中表示同一函数的是 ( )
A.f(x)=x与g(x)=( )2 )2 | B.f(x)=|x|与g(x)= |
C.f(x)=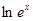 与g(x)= 与g(x)= | D.f(x)= 与g(t)=t+1(t≠1) 与g(t)=t+1(t≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知函数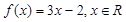 规定:给出一个实数
规定:给出一个实数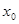 ,赋值
,赋值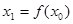 ,若
,若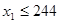 ,则继续赋值
,则继续赋值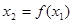 , ,
, , 以此类推,若
以此类推,若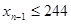 ,则
,则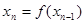 ,否则停止赋值,如果得到
,否则停止赋值,如果得到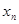 称为赋值了
称为赋值了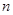 次
次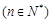 .已知赋值了
.已知赋值了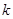 次后停止,则
次后停止,则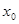 的取值范围是( )
的取值范围是( )
A.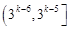 | B.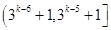 | C.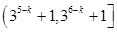 | D.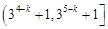 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com