
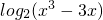 ]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;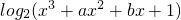 ]的图象为曲线C2,若存在实数b使得曲线C2在x0(x0∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
]的图象为曲线C2,若存在实数b使得曲线C2在x0(x0∈(1,4))处有斜率为-8的切线,求实数a的取值范围; =x3-3x,
=x3-3x,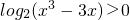 ,得x3-3x>1.又
,得x3-3x>1.又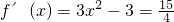 ,由f′(x)=0,得x=
,由f′(x)=0,得x= ,
, .又f(-
.又f(- )=
)= ,∴切点为(
,∴切点为( ).
). ,即15x-4y+27=0.
,即15x-4y+27=0.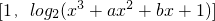 =x3+ax2+bx+1.
=x3+ax2+bx+1.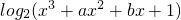 >0,得x3+ax2+bx>0,
>0,得x3+ax2+bx>0,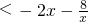 在(1,4)上有解,∴a
在(1,4)上有解,∴a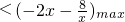 (1<x<4),
(1<x<4), =-(2x+
=-(2x+ )≤-2
)≤-2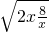 =-8,当且仅当x=2时取等号,∴a<-8.
=-8,当且仅当x=2时取等号,∴a<-8. ,
,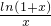 ,则
,则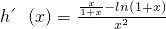 ,当x≥2时,
,当x≥2时,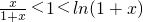 ,
,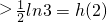 .
. ,构造函数h(x)=
,构造函数h(x)=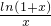 ,利用导数判断h(x)单调递减即可.
,利用导数判断h(x)单调递减即可.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:《导数及其应用》2013年高三数学一轮复习单元训练(北京邮电大学附中)(解析版) 题型:解答题
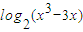 ]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程; ]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省湛江师范附中高考复习数学模拟试卷4(理科)(解析版) 题型:解答题
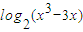 ]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;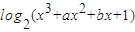 ]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com