练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知复数（x-2）+yi（x，y∈R）的模为数学公式，求数学公式的最大值．

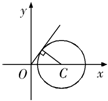
    解：∵|（x-2）+yi|=，∴（x-2）2+y2=3，故 （x，y）在以C（2，0）为圆心，
    以为半径的圆上，表示圆上的点 （x，y）与原点连线的斜率．
    如图，由平面几何知识，圆心到原点的距离等于2，圆心到切线的距离等于半径，
    易知如图所示的切线的倾斜角α=60°，
    故切线的斜率为，故的最大值为．
    分析：由题意可得 （x-2）2+y2=3，故 （x，y）在以C（2，0）为圆心，以为半径的圆上，而表示圆上的点 （x，y）与原点连线的斜率，数形结合可得的最大值．
    点评：本题主要考查复数的模的定义，直线和圆的位置关系，体现了数形结合的数学思想，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知复数（x-2）+yi（x，y∈R）的模为
    		3
    ，则
    y
    x
    的最大值是（　　）
    A、
    		3
    2
    B、
    		3
    3
    C、
    1
    2
    D、
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•宝山区一模）已知复数（x-2）+yi（x，y∈R）的模为
    		3
    ，则
    y
    x
    的最大值是
    		3
    		3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知复数（x-2）+yi（x，y∈R）的模为
    		3
    ，求
    y
    x
    的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知复数z=x-2+yi的模是2，则点（x，y）的轨迹方程是        .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知复数z=x-2+yi的模是2，则点（x，y）的轨迹方程是        .

    查看答案和解析>>

    同步练习册答案