
【题目】某养殖场需要通过某装置对养殖车间进行恒温控制,为了解日用电量![]() 与日平均气温
与日平均气温![]() (℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
(℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
日平均气温(℃) | 3 | 4 | 5 | 6 | 7 |
日用电量( | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)请利用(Ⅰ)中的线性回归方程预测日平均气温为12℃时的日用电量.
附:回归直线的斜率和截距的最小二乘法估计公式分别为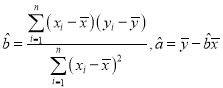 .
.
科目:高中数学 来源: 题型:
【题目】某地有种特产水果很受当地老百姓欢迎,但该种水果只能在9月份销售,且该种水果只能当天食用口感最好,隔天食用口感较差。某超市每年9月份都销售该特产水果,每天计划进货量相同,进货成本每公斤8元,销售价每公斤12元;当天未卖出的水果则转卖给水果罐头厂,但每公斤只能卖到5元。根据往年销售经验,每天需求量与当地气温范围有一定关系。如果气温不低于30度,需求量为5000公斤;如果气温位于![]() ,需求量为3500公斤;如果气温低于25度,需求量为2000公斤;为了制定今年9月份订购计划,统计了前三年9月份的气温范围数据,得下面的频数分布表
,需求量为3500公斤;如果气温低于25度,需求量为2000公斤;为了制定今年9月份订购计划,统计了前三年9月份的气温范围数据,得下面的频数分布表
气温范围 |
|
|
|
|
|
天数 | 4 | 14 | 36 | 21 | 15 |
以气温范围位于各区间的频率代替气温范围位于该区间的概率.
(1)求今年9月份这种水果一天需求量![]() (单位:公斤)的分布列和数学期望;
(单位:公斤)的分布列和数学期望;
(2)设9月份一天销售特产水果的利润为![]() (单位:元),当9月份这种水果一天的进货量为
(单位:元),当9月份这种水果一天的进货量为![]() (单位:公斤)为多少时,
(单位:公斤)为多少时,![]() 的数学期望达到最大值,最大值为多少?
的数学期望达到最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国居民生活水平的不断提高,汽车逐步进入百姓家庭,但随之面来的交通拥堵和交通事故时有发生,给人民的生活也带来了诸多不便.某市为了确保交通安全.决定对交通秩序做进步整顿,对在通路上行驶的前后相邻两机动车之间的距离d(米)与机动车行驶速度v(千米/小时)做出如下两条规定:
①![]() av2;
av2;
②![]() .(其中a是常量,表示车身长度,单位:米)
.(其中a是常量,表示车身长度,单位:米)
(1)当![]() 时.求机动车的最大行驶速度;
时.求机动车的最大行驶速度;
(2)设机动车每小时流量Q![]() ,问当机动车行驶速度v≥30(千米/小时)时,机动车以什么样的状态行驶,能使机动车每小时流量Q最大?并说明理由.(机动车每小时流量Q是指每小时通过观测点的车辆数)
,问当机动车行驶速度v≥30(千米/小时)时,机动车以什么样的状态行驶,能使机动车每小时流量Q最大?并说明理由.(机动车每小时流量Q是指每小时通过观测点的车辆数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重![]() (单位:
(单位:![]() )与身高
)与身高![]() (单位:
(单位:![]() )具有线性相关关系。根据组样本数据
)具有线性相关关系。根据组样本数据![]() ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正的线性相关关系
具有正的线性相关关系
B.回归直线过样本点的中心![]()
C.若该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]()
D.若该大学某女生身高为![]() ,则可断定其体重必为
,则可断定其体重必为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民区有一个银行网点(以下简称“网点”),网点开设了若干个服务窗口,每个窗口可以办理的业务都相同,每工作日开始办理业务的时间是8点30分,8点30分之前为等待时段.假设每位储户在等待时段到网点等待办理业务的概率都相等,且每位储户是否在该时段到网点相互独立.根据历史数据,统计了各工作日在等待时段到网点等待办理业务的储户人数,得到如图所示的频率分布直方图:
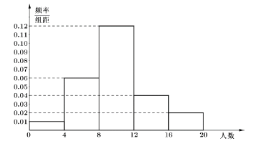
(1)估计每工作日等待时段到网点等待办理业务的储户人数的平均值;
(2)假设网点共有1000名储户,将频率视作概率,若不考虑新增储户的情况,解决以下问题:
①试求每位储户在等待时段到网点等待办理业务的概率;
②储户都是按照进入网点的先后顺序,在等候人数最少的服务窗口排队办理业务.记“每工作日上午8点30分时网点每个服务窗口的排队人数(包括正在办理业务的储户)都不超过3”为事件![]() ,要使事件
,要使事件![]() 的概率不小于0.75,则网点至少需开设多少个服务窗口?
的概率不小于0.75,则网点至少需开设多少个服务窗口?
参考数据:![]() ;
;![]() ;
;
![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() (
(![]() ,
,![]() )的右焦点
)的右焦点![]() ,且椭圆
,且椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() 的面积
的面积![]() .
.
①求证:![]() 为定值;
为定值;
②设直线![]() 的中点
的中点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com