
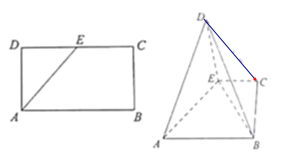
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形,![]() ,
, ![]() ,
,![]() ,
,![]() , 且
, 且![]() ,
,![]() ,
,![]()
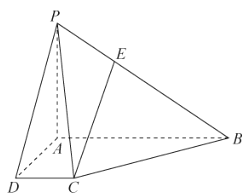
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离;
的距离;
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的三等分点
的三等分点![]() ,法一,利用线面平行的判定定理证明.法二,利用面面平行判定定理证明;
,法一,利用线面平行的判定定理证明.法二,利用面面平行判定定理证明;
(2)法一,利用等积转换即![]() ,即可求得,法二,利用空间向量法,求点到面的距离.
,即可求得,法二,利用空间向量法,求点到面的距离.
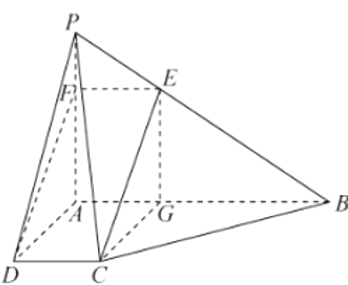
(1)解法一:取![]() 的三等分点
的三等分点![]() ,连结
,连结![]() ,则
,则![]()
又因为![]() ,所以
,所以![]() 且
且![]() ,
,
因为![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,
,
又平面![]() 平面
平面 ![]() ,
,![]() 平面
平面 ![]() ,
,
所以![]() 平面
平面 ![]() .
.
解法二:取![]() 的三等分点
的三等分点![]() ,连结
,连结![]() ,则
,则![]() ,
,
又因为![]() ,
,
所以![]() 且
且![]() ,
,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
因为![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
四边形![]() 是平行四边形.
是平行四边形.
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解法一:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以,![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
点![]() 平面
平面![]() 的距离是
的距离是![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
因为![]() ,所以,
,所以,![]()
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
因为![]() ,
,![]() ,所以
,所以![]()
所以,![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
分别以![]() 为
为![]() 轴
轴![]() 轴
轴![]() 轴,建立空间坐标系,
轴,建立空间坐标系,
![]() ’
’![]() ,
,
设平面![]() 法向量
法向量![]() ,
,
因为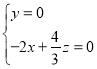 ,所以
,所以![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() , 则
, 则
点![]() 到平面
到平面![]() 的距离
的距离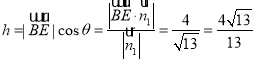 ,
,
点![]() 到平面
到平面![]() 的距离为
的距离为 ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=4,AD=2,点E是DC的中点,将△ADE沿AE折起,使平面ADE⊥平面ABCE,连结DB、DC、EB.
(1)求证:平面ADE⊥平面BDE;
(2)求AD与平面BDC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“北京八分钟”在韩国平昌冬奥会惊艳亮相,冬奥会正式进入了北京周期,全社会对冬奥会的热情空前高涨.
(1)为迎接冬奥会,某社区积极推动冬奥会项目在社区青少年中的普及,并统计了近五年来本社区冬奥项目青少年爱好者的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年),列表如下:
(单位:年),列表如下:

依据表格给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).
并加以说明(计算结果精确到0.01).
(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式 ,参考数据
,参考数据![]() .
.
(2)某冰雪运动用品专营店为吸引广大冰雪爱好者,特推出两种促销方案.
方案一:每满600元可减100元;
方案二:金额超过600元可抽奖三次,每次中奖的概率同为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
两位顾客都购买了1050元的产品,并且都选择第二种优惠方案,求至少有一名顾客比选择方案一更优惠的概率;
②如果你打算购买1000元的冰雪运动用品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】丑橘是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的丑橘,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 | 150 | 160 | 140 | 155 | 170 |
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的丑橘中随机抽取一箱,估计该箱丑橘价格低于160元的概率;
(2)按市场份额进行分层抽样,随机抽取20箱丑橘进行检验,①从产地![]() ,
,![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;②从这
的值;②从这![]() 箱中随机抽取三箱进行等级检验,随机变量
箱中随机抽取三箱进行等级检验,随机变量![]() 表示来自产地
表示来自产地![]() 的箱数,求
的箱数,求![]() 的分布列和数学期望.
的分布列和数学期望.
(3)产地![]() 的丑橘明年将进入该地市场,定价160元/箱,并占有一定市场份额,原有五个产地的丑橘价格不变,所占市场份额之比不变(不考虑其他因素).设今年丑橘的平均批发价为每箱
的丑橘明年将进入该地市场,定价160元/箱,并占有一定市场份额,原有五个产地的丑橘价格不变,所占市场份额之比不变(不考虑其他因素).设今年丑橘的平均批发价为每箱![]() 元,明年丑橘的平均批发价为每箱
元,明年丑橘的平均批发价为每箱![]() 元,比较
元,比较![]() ,
,![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com