解(1):(Ⅰ)令a
x=t,x>0,因为a>1,所以t>1,
所以关于x的方程f(x)=m有两个不同的正数解等价关于t的方程
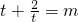
有相异的且均大于1的两根,即关于t的方程t
2-mt+2=0有相异的且均大于1的两根,所以

,解得

,
故实数m的取值范围为区间
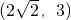
.
(Ⅱ)g(x)=a
|x|+2a
x,x∈[-2,+∞)
①当a>1时,
(a)x≥0时,a
x≥1,g(x)=3a
x,所以g(x)∈[3,+∞),
(b)-2≤x<0时,

g(x)=a
-x+2a
x,所以
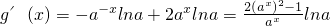
ⅰ当
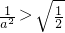
即
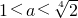
时,对?x∈(-2,0),g'(x)>0,所以g(x)在[-2,0)上递增,
所以
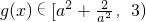
,综合(a)(b),g(x)有最小值为
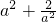
与a有关,不符合
ⅱ当
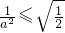
即
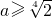
时,由g'(x)=0得
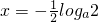
,
且当
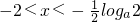
时g'(x)<0,
当
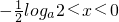
时,g'(x)>0,
所以g(x)在
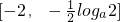
上递减,在
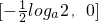
上递增,
所以

=

,综合(a)(b)g(x)有最小值为

与a无关,符合要求.
②当0<a<1时,
(a)x≥0时,0<a
x≤1,g(x)=3a
x,所以g(x)∈(0,3]
(b)-2≤x<0时,
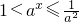
,g(x)=a
-x+2a
x,
所以
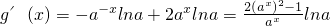
<0,g(x)在[-2,0)上递减,
所以
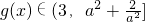
,综合(a)(b)g(x)有最大值为
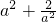
与a有关,不符合
综上所述,实数a的取值范围是
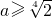
.
(2)解:(Ⅰ)
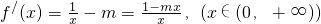
当m≤0时,f
/(x)>0恒成立,则函数f(x)在(0,+∞)上单调递增;
当m>0时,由
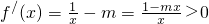
则
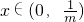
,则f(x)在
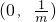
上单调递增,在
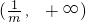
上单调递减.
(Ⅱ)由(Ⅰ)得:当m≤0时显然不成立;
当m>0时,
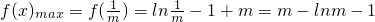
只需m-lnm-1≤0即令g(x)=x-lnx-1,
则
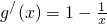
,函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
∴g(x)
min=g(1)=0
则若f(x)≤0在x∈(0,+∞)上恒成立,m=1.
(Ⅲ)
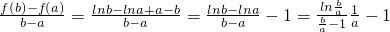
,
由0<a<b得
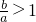
,由(Ⅱ)得:
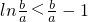
,
则
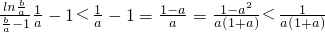
,
则原不等式
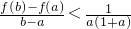
成立.
分析:(1):(Ⅰ)令a
x=t利用换元法把方程化简,方程f(x)=m有两个不同的正数解等价于关于t的方程有相异的且均大于1的两根列出不等式求出解集即可;
(Ⅱ)根据题意得到g(x),分a>1和0<a<1两种情况利用导函数的增减性求出函数的最值,找出与a无关的范围即可;
(2):(Ⅰ)求出f′(x)讨论其大于0得到函数的单调增区间,小于0得到函数的单调减区间即可;
(Ⅱ)由于f(x)≤0在x∈(0,+∞)上恒成立,就是要f(x)的最小值小于等于0,利用(Ⅰ)的结论得到函数的最大值,求出m即可;
(Ⅲ)利用利用(Ⅱ)的结论化简不等式左边利用(Ⅱ)结论得证.
点评:此题是一道综合题,考查学生对函数最值及几何意义的理解,利用导数研究函数增减性及最值的能力,以及函数与方程的综合运用能力.

 ,
,
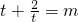 有相异的且均大于1的两根,即关于t的方程t2-mt+2=0有相异的且均大于1的两根,所以
有相异的且均大于1的两根,即关于t的方程t2-mt+2=0有相异的且均大于1的两根,所以 ,解得
,解得 ,
,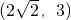 .
. g(x)=a-x+2ax,所以
g(x)=a-x+2ax,所以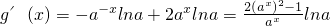
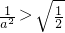 即
即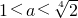 时,对?x∈(-2,0),g'(x)>0,所以g(x)在[-2,0)上递增,
时,对?x∈(-2,0),g'(x)>0,所以g(x)在[-2,0)上递增,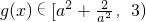 ,综合(a)(b),g(x)有最小值为
,综合(a)(b),g(x)有最小值为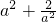 与a有关,不符合
与a有关,不符合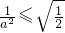 即
即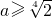 时,由g'(x)=0得
时,由g'(x)=0得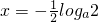 ,
,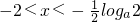 时g'(x)<0,
时g'(x)<0,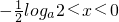 时,g'(x)>0,
时,g'(x)>0,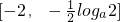 上递减,在
上递减,在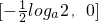 上递增,
上递增, =
= ,综合(a)(b)g(x)有最小值为
,综合(a)(b)g(x)有最小值为 与a无关,符合要求.
与a无关,符合要求.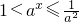 ,g(x)=a-x+2ax,
,g(x)=a-x+2ax,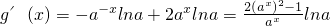 <0,g(x)在[-2,0)上递减,
<0,g(x)在[-2,0)上递减,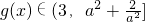 ,综合(a)(b)g(x)有最大值为
,综合(a)(b)g(x)有最大值为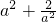 与a有关,不符合
与a有关,不符合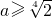 .
.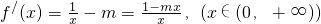
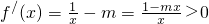
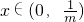 ,则f(x)在
,则f(x)在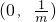 上单调递增,在
上单调递增,在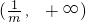 上单调递减.
上单调递减.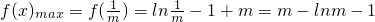 只需m-lnm-1≤0即令g(x)=x-lnx-1,
只需m-lnm-1≤0即令g(x)=x-lnx-1,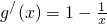 ,函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
,函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.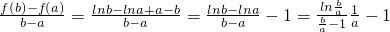 ,
,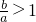 ,由(Ⅱ)得:
,由(Ⅱ)得: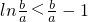 ,
,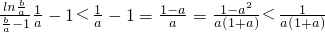 ,
,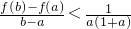 成立.
成立.

 阅读快车系列答案
阅读快车系列答案