
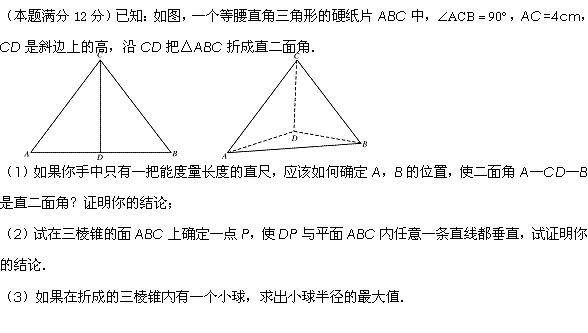
解析:(1)用直尺度量折后的AB长,若AB=4cm,则二面角A―CD―B为直二面角.
∵△ABC是等腰直角三角形,∴AD=DB=CD=2![]() cm.. 又∵AD⊥DC,BD⊥DC,
cm.. 又∵AD⊥DC,BD⊥DC,
∴∠ADB是二面角A―CD―B的平面角.∵AD=DB=![]() cm,当AB=4cm时,有AD2+DB2=AB2,
cm,当AB=4cm时,有AD2+DB2=AB2,
∴∠ADB=90°,即二面角A―CD―B为直二面角.(5分)
(2)取△ABC的中心P,连结DP,则DP满足条件.∵△ABC为正三角形,且AD=DB=DC,
∴三棱锥D―ABC是正三棱锥.,由P为△ABC的中心,则DP⊥平面ABC.∴DP与平面ABC内任意一条直线都垂直.(10分)
(3)当小球半径最大时,此小球与三棱锥的四个面都相切. 设小球球心为O,半径为r,连结OA,OB,OC,OD,则三棱锥被分为四个小棱锥,则有
![]() ,
,
即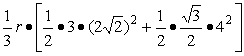 =
=![]()
即![]()
∴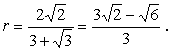 故小球半径最大值为
故小球半径最大值为![]() 分(14
分(14


科目:高中数学 来源: 题型:
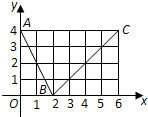 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com