
【题目】已知定义在R上的偶函数f(x),满足f(x+4)=-f(x)+f(2),且在区间[0,4]上是增函数,下列命题中正确的是( )
A.函数f(x)的一个周期为4
B.直线x=-4是函数f(x)图象的一条对称轴
C.函数f(x)在[-6,-5)上单调递增,在[-5,-4)上单调递减
D.函数f(x)在[0,100]内有25个零点
科目:高中数学 来源: 题型:
【题目】现某路口对一周内过往人员进行健康码检查安排7名工作人员进行值班,每人值班1天,每天1人,其中甲乙两人需要安排在相邻两天,且甲不排在周三,则不同的安排方法有( )
A.1440种B.1400种C.1320种D.1200种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量![]() =(sinA+sinC,sinB),
=(sinA+sinC,sinB),![]() =(c﹣b,c﹣a),且
=(c﹣b,c﹣a),且![]() ∥
∥![]() .
.
(1)求角A的大小;
(2)若a=3,b+c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 |
|
|
|
|
|
管理时间 |
|
|
|
|
|
并调查了某村![]() 名村民参与管理的意愿,得到的部分数据如下表所示:
名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 |
|
|
女性村民 |
|
![]() 求出相关系数
求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
![]() 若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取
若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取![]() 人,记取到不愿意参与管理的男性村民的人数为
人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx2+(1-3m)x-4,m∈R.
(1)当m=1时,求f(x)在区间[-2,2]上的最大值和最小值.
(2)解关于x的不等式f(x)>-1.
(3)当m<0时,若存在x0∈(1,+∞),使得f(x)>0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1) 已知函数![]() ,若
,若![]() ,则
,则![]() _____.
_____.
(2)等差数列{an}的前n项和为Sn,若a2=2,a11-a4=7,则S13=________.
(3)若命题“x∈R,使得x2+(a﹣1)x+1<0”是真命题,则实数a的取值范围是______.
(4)在△ABC中,tanA+tanB+![]() =
=![]() tanA·tanB,且sinA·cosA=
tanA·tanB,且sinA·cosA=![]() ,则此三角形为_______.
,则此三角形为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 函数
函数![]() 与直线
与直线![]() 相切,设函数
相切,设函数![]() 其中a、c∈R,e是自然对数的底数.
其中a、c∈R,e是自然对数的底数.
(1)讨论h(x)的单调性;
(2)h(x)在区间![]() 内有两个极值点.
内有两个极值点.
①求a的取值范围;
②设函数h(x)的极大值和极小值的差为M,求实数M的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
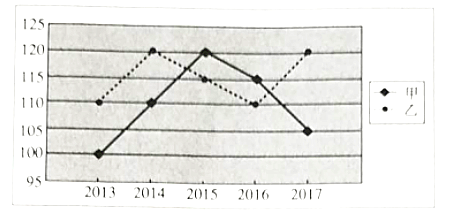
(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: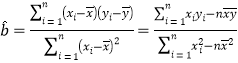 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com