Question

将一块边长为42cm的正方形铁皮剪去四个角（四个全等的小正方形）做成一个无盖铁盒，要使其容积最大，剪去的小正方形的边长为 7 cm．

Answer 1

【答案】分析：首先由题意建立起无盖铁盒的体积函数，变形成为（42-2x）•（42-2x）•4x，分析得到其“和”是定值，联想到利用基本不等式利用求最值，当且仅当a=b=c时取等．
解答：解：设剪去的小正方形的边长为xcm，则无盖铁盒体积V=（42-2x）²•x．
所以：V=（42-2x）²•x=•（42-2x）•（42-2x）•4x=•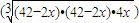³≤•[]³
=•28³，当且仅当42-2x=4x时，即x=7时取得最大值．
故答案为：7．
点评：此题主要考查利用基本不等式求最值在实际问题中的应用．前提是“一正二定三相等”，需通过变形技巧，得到“和”或“积”为定值的情形．然后应用不等式即可．