
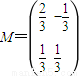 ,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积.
,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积. .
.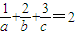 ,求a+2b+3c的最小值及取得最小值时a,b,c的值.
,求a+2b+3c的最小值及取得最小值时a,b,c的值.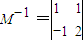 ,(3分)
,(3分) ,
, ,
,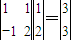 ,
,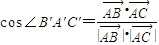
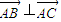 .
.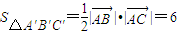 ,(7分)
,(7分)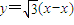 ,(2分)
,(2分)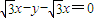 的距离为2.
的距离为2.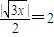 ,解得
,解得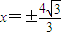 .(7分)
.(7分)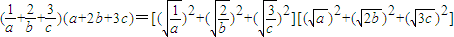
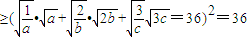 .(5分)
.(5分)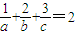 ,∴a+2b+3c≥18.当且仅当
,∴a+2b+3c≥18.当且仅当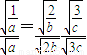 ,
,

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
查看答案和解析>>
科目:高中数学 来源:2010年淮安市淮阴区高二下学期期末考试数学卷 题型:解答题
已知矩阵
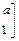 ,a为实数,若点(1,-2)在矩阵A的变换下得到点(-4,0)
,a为实数,若点(1,-2)在矩阵A的变换下得到点(-4,0)
(1)求实数a的值 (2)求矩阵A的特征值及其对应的特征向量。
查看答案和解析>>
科目:高中数学 来源:2010年淮安市淮阴区高二下学期期末考试数学卷 题型:解答题
已知矩阵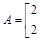
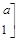 ,a为实数,若点(1,-2)在矩阵A的变换下得到点(-4,0)
,a为实数,若点(1,-2)在矩阵A的变换下得到点(-4,0)
(1)求实数a的值 (2)求矩阵A的特征值及其对应的特征向量。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州市江都市大桥中学高一(下)期中数学试卷(解析版) 题型:解答题
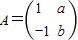 ,A的一个特征值λ=2,属于λ的特征向量是
,A的一个特征值λ=2,属于λ的特征向量是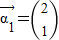 ,求矩阵A与其逆矩阵.
,求矩阵A与其逆矩阵.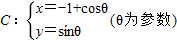 上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com