练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求值:sin210°+cos240°+sin10°cos40°.

    思路分析:由c2=a2+b2-2abcosC,可得sin2C=sin2A+sin2B-2sinAsinBcosC,对此可得如下解法.

    解:sin210°+cos240°+sin102cos40°=sin210°+sin250°+sin10°sin50°.

    在△ABC中,令A=10°,B=50°,C=120°,

    由余弦定理:

    c2=a2+b2-2abcosC,

    再由正弦定理:

    (2Rsin120°)2=(2Rsin10°)2+(2Rsin50°)2-2(4R2sin10°sin50°)cos120°,

    即得sin210°+sin250°+sin10°sin50°=.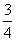

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    求值sin210°=（　　）
    A、
    		3
    2
    B、-
    		3
    2
    C、
    1
    2
    D、-
    1
    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求
    cos190°•(-sin210°)cos350°•(-tan585°)
    的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求值：sin210°+cos120°+tan225°=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省泉州市师院附属鹏峰中学高一（下）期中数学试卷（解析版） 题型：填空题

    求值：sin210°+cos120°+tan225°=    ．

    查看答案和解析>>

    同步练习册答案