
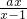 )<f(2),试求x的取值范围.
)<f(2),试求x的取值范围. 可以解得x>1或x<0. (2分)
可以解得x>1或x<0. (2分)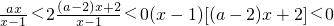 (2分)
(2分) ; (3分)
; (3分) .(3分)
.(3分)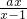 )<f(2),我们可得到一个关于x的不等式(含参数a),根据二次不等式的解法,分a=2时,0<a<2时和当a>2时,三种情况讨论,即可得到x的取值范围.
)<f(2),我们可得到一个关于x的不等式(含参数a),根据二次不等式的解法,分a=2时,0<a<2时和当a>2时,三种情况讨论,即可得到x的取值范围.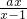 )<f(2),转化为(x-1)[(a-2)x+2]<0是解答本题的关键,本题易忽略a=2时的情况,造成答案的不完整!
)<f(2),转化为(x-1)[(a-2)x+2]<0是解答本题的关键,本题易忽略a=2时的情况,造成答案的不完整! 

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
| x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2(x-1) | x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com