
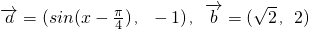 且
且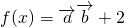
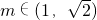 ,求x1+x2的值.
,求x1+x2的值.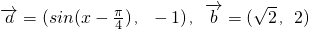 ,
,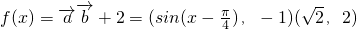 +2
+2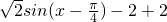 =
= .
.
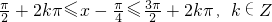
 .
.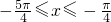 ;当k=0时,得
;当k=0时,得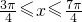 .
.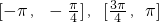 .
.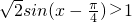 ,得
,得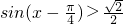 .
. .
.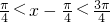 ,则
,则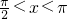 .
.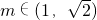 时方程f(x)=m的两个根x1,x2关于x=
时方程f(x)=m的两个根x1,x2关于x= 对称.
对称. .
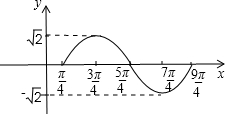
.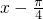 分别取0,
分别取0, ,π,
,π, ,2π求出x的值进行列表,然后描点用平滑曲线连接;
,2π求出x的值进行列表,然后描点用平滑曲线连接;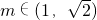 时关于x的方程f(x)=m在x∈[-π,π]上的根x1,x2在
时关于x的方程f(x)=m在x∈[-π,π]上的根x1,x2在 内切关于x=
内切关于x= 对称,利用中点坐标公式求x1+x2的值.
对称,利用中点坐标公式求x1+x2的值.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源:2012-2013学年湖北省襄阳市襄州、枣阳、宜城、曾都一中联考高三(上)期中数学试卷(文科)(解析版) 题型:解答题
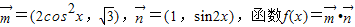 .
.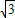 ,且a>b,求a,b的值.
,且a>b,求a,b的值.查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京市101中学高一(上)期末数学试卷(理科)(解析版) 题型:解答题
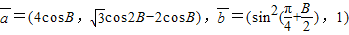 ,
,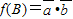
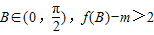 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省株洲市攸县二中高三数学试卷11(文科)(解析版) 题型:解答题
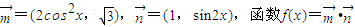 .
.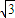 ,且a>b,求a,b的值.
,且a>b,求a,b的值.查看答案和解析>>
科目:高中数学 来源:2010-2011年河北冀州中学高一年级下学期期末考试理科数学(B卷) 题型:解答题
(本小题满分12分)已知向量
 。
。
(1)若f(x)=1,求cos(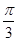 +x)的值;
+x)的值;
(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,
求函数f(A)的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com