|
|
|
已知集合A={x∈R|f|x|≠0},集合B={x∈R|g(x)≠0},全集U=R,则集合{x|f2(x)+g2(x)=0}=
|
| [ ] |
A. |
( UA)∩( UA)∩( UB) UB)
|
B. |
( UA)∪( UA)∪( UB) UB)
|
C. |
 U(A∪B) U(A∪B)
|
D. |
A∩ UB UB
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N+
(1)证明:数列 是等差数列; 是等差数列;
(2)设 ,求数列{bn}的前n项和Sn. ,求数列{bn}的前n项和Sn.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
下列四个命题:
①若m∈(0,1],则函数 的最小值为 的最小值为 ; ;
②已知平面α,β,直线l,m,若l⊥α,m β,α⊥β,则l∥m; β,α⊥β,则l∥m;
③△ABC中, 和 和 的夹角等于180°-A; 的夹角等于180°-A;
④若动点P到点F(1,0)的距离比到直线l:x=-2的距离小1,则动点P的轨迹方程为y2=4x.
其中正确命题的序号为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知x>0,y>0,若 + + >m2+2 m恒成立,则实数m的取值范围是 >m2+2 m恒成立,则实数m的取值范围是
|
| [ ] |
A. |
m≥4或m≤-2
|
B. |
m≥2或m≤-4
|
C. |
-2<m<4
|
D. |
-4<m<2
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-1,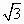 ). ).
(Ⅰ)求sin2α-tanα的值;
(Ⅱ)若函数f(x)=cos(x+α)cosα+sin(x+α)sinα,求函数g(x)=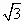 f( f( -2x)-2f2(x)+1在区间[0, -2x)-2f2(x)+1在区间[0, ]上的取值范围. ]上的取值范围.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
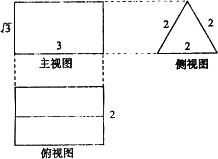
下图是一个几何体的三视图.已知侧视图是一个等边三角形,根据图中尺寸(单位:cm);可知这个几何体的表面积是
|
| [ ] |
A. |
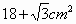
|
B. |
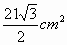
|
C. |
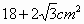
|
D. |
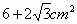
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
由函数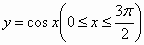 的图象与直线 的图象与直线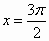 及y=1,所围成的一个封闭图形的面积是________. 及y=1,所围成的一个封闭图形的面积是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数y=f(x)在R上可导,且满足不等x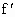 (x)>-f(x)恒成立,常数a,b满足a>b则下列不等式一定成立的是 (x)>-f(x)恒成立,常数a,b满足a>b则下列不等式一定成立的是
|
| [ ] |
A. |
af(b)>bf(a)
|
B. |
af(a)>bf(b)
|
C. |
af(a)<bf(b)
|
D. |
af(b)<bf(a)
|
|
|
查看答案和解析>>
