
 如图,菱形ABCD所在平面与矩形ACEF所在平面互相垂直,已知BD=2AF,且点M是线段EF的中点.
如图,菱形ABCD所在平面与矩形ACEF所在平面互相垂直,已知BD=2AF,且点M是线段EF的中点.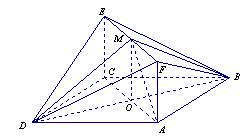 解:(Ⅰ)设AC∩BD=O,连OE.
解:(Ⅰ)设AC∩BD=O,连OE. AC=AO,
AC=AO, BD=AF=MO
BD=AF=MO

科目:高中数学 来源: 题型:
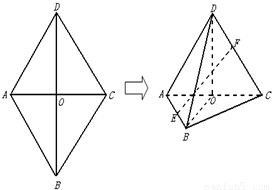
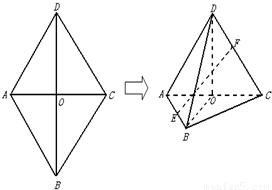
 (2012•闸北区二模)如图,菱形ABCD中,AB=AC=1,其对角线的交点为O,现将△ADC沿对角线AC向上翻折,使得OD⊥OB.在四面体ABCD中,E在AB上移动,点F在DC上移动,且AE=CF=a(0≤a≤1).
(2012•闸北区二模)如图,菱形ABCD中,AB=AC=1,其对角线的交点为O,现将△ADC沿对角线AC向上翻折,使得OD⊥OB.在四面体ABCD中,E在AB上移动,点F在DC上移动,且AE=CF=a(0≤a≤1).查看答案和解析>>
科目:高中数学 来源: 题型:
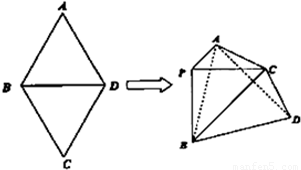
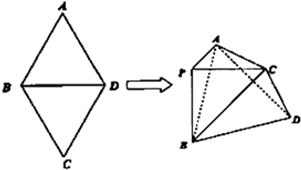 如图,菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,空间中的点P满足PA、PB、PC两两垂直,则下列命题中错误的是( )
如图,菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,空间中的点P满足PA、PB、PC两两垂直,则下列命题中错误的是( )查看答案和解析>>
科目:高中数学 来源:2012年云南省昆明市高三复习适应性检测数学试卷(理科)(解析版) 题型:选择题

查看答案和解析>>
科目:高中数学 来源:2012年上海市高考数学压轴试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012年上海市闸北区高考数学二模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com