
已知椭圆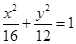 ,则以点
,则以点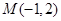 为中点的弦所在直线方程为__________________。
为中点的弦所在直线方程为__________________。
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| RP |
| PF2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市高新区高三2月月考理科数学试卷(解析版 题型:填空题
已知椭圆方程为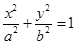 (
(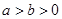 ),F
),F (-c,0)和F
(-c,0)和F (c,0)分别是椭圆的左 右焦点.
(c,0)分别是椭圆的左 右焦点.
①若P是椭圆上的动点,延长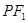 到M,使
到M,使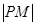 =
=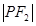 ,则M的轨迹是圆;
,则M的轨迹是圆;
②若P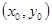 是椭圆上的动点,则
是椭圆上的动点,则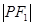
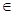
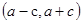 ;
;
③以焦点半径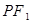 为直径的圆必与以长轴为直径的圆内切;
为直径的圆必与以长轴为直径的圆内切;
④若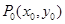 在椭圆
在椭圆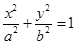 上,则过
上,则过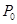 的椭圆的切线方程是
的椭圆的切线方程是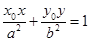 ;
;
⑤点P为椭圆上任意一点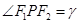 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为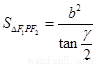 .
.
以上说法中,正确的有
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高考模拟试题(1) 题型:解答题
已知椭圆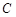 :
: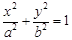 (
(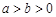 ),其焦距为
),其焦距为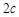 ,若
,若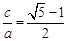 (
(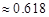 ),则称椭圆
),则称椭圆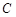 为“黄金椭圆”.
为“黄金椭圆”.
(1)求证:在黄金椭圆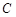 :
: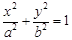 (
(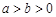 )中,
)中,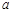 、
、 、
、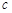 成等比数列.
成等比数列.
(2)黄金椭圆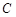 :
: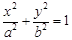 (
(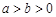 )的右焦点为
)的右焦点为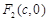 ,
,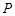 为椭圆
为椭圆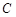 上的
上的
任意一点.是否存在过点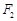 、
、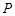 的直线
的直线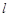 ,使
,使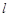 与
与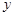 轴的交点
轴的交点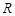 满足
满足 ?若存在,求直线
?若存在,求直线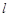 的斜率
的斜率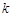 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)在黄金椭圆中有真命题:已知黄金椭圆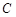 :
: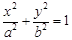 (
(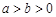 )的左、右焦点分别是
)的左、右焦点分别是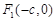 、
、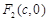 ,以
,以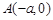 、
、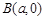 、
、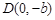 、
、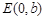 为顶点的菱形
为顶点的菱形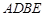 的内切圆过焦点
的内切圆过焦点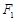 、
、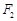 .试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
查看答案和解析>>
科目:高中数学 来源:2010年上海市卢湾区高考数学二模试卷(理科)(解析版) 题型:解答题
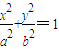 (a>b>0),其焦距为2c,若
(a>b>0),其焦距为2c,若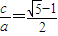 (≈0.618),则称椭圆C为“黄金椭圆”.
(≈0.618),则称椭圆C为“黄金椭圆”.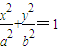 (a>b>0)中,a、b、c成等比数列.
(a>b>0)中,a、b、c成等比数列.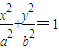 (a>b>0)的右焦点为F2(c,0),P为椭圆C上的任意一点.是否存在过点F2、P的直线l,使l与y轴的交点R满足
(a>b>0)的右焦点为F2(c,0),P为椭圆C上的任意一点.是否存在过点F2、P的直线l,使l与y轴的交点R满足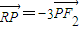 ?若存在,求直线l的斜率k;若不存在,请说明理由.
?若存在,求直线l的斜率k;若不存在,请说明理由.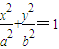 (a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),以A(-a,0)、B(a,0)、D(0,-b)、E(0,b)为顶点的菱形ADBE的内切圆过焦点F1、F2.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),以A(-a,0)、B(a,0)、D(0,-b)、E(0,b)为顶点的菱形ADBE的内切圆过焦点F1、F2.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.查看答案和解析>>
科目:高中数学 来源:2010年上海市卢湾区高考模拟考试(理) 题型:解答题
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆 :
: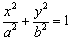 (
( ),其焦距为
),其焦距为 ,若
,若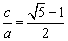 (
(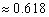 ),则称椭圆
),则称椭圆 为“黄金椭圆”.
为“黄金椭圆”.
(1)求证:在黄金椭圆 :
: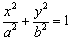 (
( )中,
)中,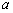 、
、 、
、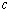 成等比数列.
成等比数列.
(2)黄金椭圆 :
: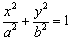 (
( )的右焦点为
)的右焦点为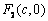 ,
, 为椭圆
为椭圆 上的
上的
任意一点.是否存在过点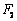 、
、 的直线
的直线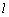 ,使
,使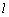 与
与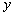 轴的交点
轴的交点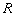 满足
满足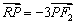 ?若存在,求直线
?若存在,求直线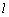 的斜率
的斜率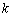 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)在黄金椭圆中有真命题:已知黄金椭圆 :
: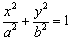 (
( )的左、右
)的左、右
焦点分别是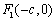 、
、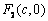 ,以
,以 、
、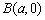 、
、 、
、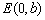 为顶点的菱形
为顶点的菱形 的内切圆过焦点
的内切圆过焦点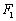 、
、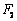 .
.
试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com