练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    矩阵N=的特征值为 ．

     

    ﹣3，8．

    【解析】

    试题分析：令矩阵M的特征多项式等于0，即可求得矩阵M的特征值．

    【解析】
    矩阵M的特征多项式为f（λ）==λ2﹣5λ﹣24

    令f（λ）=0可得λ=﹣3或λ=8，

    即矩阵M的特征值为﹣3或8．

    故答案为：﹣3，8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2015年人教A版选修1-1 3.4生活中的优化问题举例练习卷（解析版） 题型：填空题

    做一个无盖的圆柱形水桶，若要使体积是27π，且用料最省，则圆柱的底面半径为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2015人教B版选修4-5 3.2用数学归纳法证明不等式练习卷（解析版） 题型：选择题

    已知x∈R+，不等式x+≥2，x+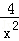≥3，…，可推广为x+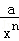≥n+1，则a的值为（ ）

    A.2n B.n2 C.22（n﹣1） D.nn

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-6 2.3费马小定理和欧拉定理练习卷（解析版） 题型：解答题

    证明：对任给的奇素数p，总存在无穷多个正整数n使得p|（n2n﹣1）．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量（解析版） 题型：填空题

    已知矩阵M=的一个特征值为﹣1，则其另一个特征值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量（解析版） 题型：填空题

    （2014•闸北区三模）将正整数1，2，3，4，…，n2（n≥2）任意排成n行n列的数表．对于某一个数表，计算各行和各列中的任意两个数a，b（a＞b）的比值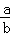，称这些比值中的最小值为这个数表的“特征值”．若aij表示某个n行n列数表中第i行第j列的数（1≤i≤n，1≤j≤n），且满足aij=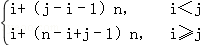，当n=4时数表的“特征值”为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：填空题

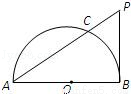
    （2014•清远一模）如图，O是半圆的圆心，直径AB=2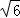，PB是圆的一条切线，割线PA与半圆交于点C，AC=4，则PB= ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

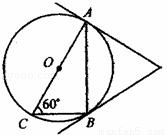
    如图，AC是⊙O的直径，∠ACB=60°，连接AB，过A、B两点分别作⊙O的切线，两切线交于点P．若已知⊙O的半径为1，则△PAB的周长为（ ）

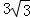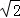    A. B. C.3 D.2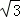

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷（解析版） 题型：选择题

    设复数z=1+i（i是虚数单位），则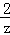+z2=（ ）

    A.﹣1﹣i B.﹣1+i C.1﹣i D.1+i

     

    查看答案和解析>>

    同步练习册答案