
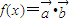 ,
,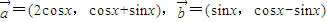 .
.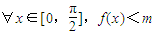 ,求实数m的取值范围.
,求实数m的取值范围.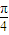 的范围,再由三角函数的图象可得答案.
的范围,再由三角函数的图象可得答案.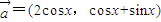 ,
,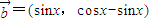 ,
,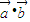 =2cosxsinx+(cosx+sinx)(cosx-sinx)
=2cosxsinx+(cosx+sinx)(cosx-sinx)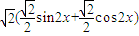 =
=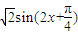
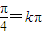 ,则x=
,则x=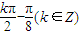
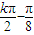 ,0)(k∈Z)
,0)(k∈Z)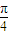 =k
=k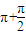 ,则得,x=
,则得,x=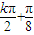 ,(k∈Z)
,(k∈Z)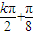 ,(k∈Z)
,(k∈Z)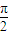 ∴
∴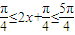
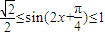
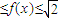 ∴m
∴m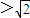
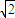 ,+∞)
,+∞)

科目:高中数学 来源: 题型:
| x2+ax+b |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年高三(上)期末数学试卷(文科)(解析版) 题型:解答题
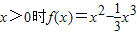
 上的值域为
上的值域为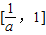 ,求a的值.
,求a的值.查看答案和解析>>
科目:高中数学 来源:2014届度河南省许昌六校高一上学期第一次联考数学试卷 题型:解答题
设函数y=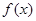 是定义在(0,+∞)上的增函数,并满足
是定义在(0,+∞)上的增函数,并满足
1、求f(1)的值;
2、若存在实数m,使 ,求m的值
,求m的值
3、如果 <2求x的范围
<2求x的范围
查看答案和解析>>
科目:高中数学 来源:2010年北京市朝阳外国语学校高考数学模拟试卷(一)(解析版) 题型:解答题
 ,若函数
,若函数 且
且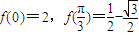 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com