对于数列{un}若存在常数M＞0，对任意的n∈N'，恒有|un+1-un|+|un-un-1|+…+|u2-u1|≤M
则称数列{un}为B-数列
（1）首项为1，公比为q（|q|＜1）的等比数列是否为B-数列？请说明理由；
（2）设Sn是数列{xn}的前n项和，给出下列两组论断；
A组：①数列{xn}是B-数列 ②数列{xn}不是B-数列
B组：③数列{Sn}是B-数列 ④数列{Sn}不是B-数列
请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题．
判断所给命题的真假，并证明你的结论；
（3）若数列{an}，{bn}都是B-数列，证明：数列{anbn}也是B-数列．
分析：（1）根据B-数列的定义，首项为1，公比为q（|q|＜1）的等比数列，验证|un+1-un|+|un-un-1|+…+|u2-u1|≤M即可；
（2）首项写出两个命题，根据B-数列的定义加以证明，如果要说明一个命题不正确，则只需举一反例即可；
（3）数列{an}，{bn}都是B-数列，则有|an+1-an|+|an-an-1|+…+|a2-a1|≤M1，|bn+1-bn|+|bn-an-1|…++|b2-b1|≤M2，下面只需验证|an+1bn+1-anbn|+|anbn-an-1bn-1|+…+|a2b2-a1b1|≤M．
解答：解（1）设满足题设的等比数列为{a
n}，则a
n=q
n-1，于是|a
n-a
n-1|=|q
n-1-q
n-2|=|q|
n-2|q-1|，n≥2
因此|a
n+1-a
n|+|a
n-a
n-1|+…+|a
2-a
1|=|q-1|（1+|q|+|q|
2++|q|
n-1）．
因为|q|＜1，所以1+|q|+|q|
2+…+|q|
n-1=
＜，即|a
n+1-a
n|+|a
n-a
n1|+…+|a
2-a
1|＜
故首项为1，公比为q（|q|＜1）的等比数列是B-数列．
（2）命题1：若数列{x
n}是B-数列，则数列{S
n}是B-数列．
此命题为假命题．
事实上，设x
n=1，n∈N
•，易知数列{x
n}是B-数列，但S
n=n|S
n-1-S
n|+|S
n-S
n+1|+…+|S
2-S
1|=n
由n的任意性知，数列{S
n}是B-数列此命题为假命题．
命题2：若数列{S
n}是B-数列，则数列{x
n}是B-数列
此命题为真命题
事实上，因为数列{S
n}是B-数列，
所以存在正数M，对任意的n∈N
*，有|S
n+1-S
n|+|S
n-S
n-1|+…+|S
2-S
1|≤M
即|x
n+1|+|x
n|+…+|x
2|≤M．
于是|x
n+1-x
n|+|x
n-x
n-1|+…+|x
2-x
1|≤|x
n+1|+2|x
n|+2|x
n-1|+…+2|x
2|+2|x
1|≤2M+|x
1|
所以数列{x
n}是B-数列．
（3）若数列{a
n}{b
n}是B-数列，则存在正数M
1．M
2，
对任意的n∈N
•，有|a
n+1-a
n|+|a
n-a
n-1|+…+|a
2-a
1|≤M
1，|b
n+1-b
n|+|b
n-a
n-1|…++|b
2-b
1|≤M
2注意到|a
n|=|a
n-a
n-1+a
n-1+a
n-2+…+a
2-a
1+a
1|≤|a
n-a
n-1|+|a
n-1-a
n-2|+…+|a
2-a
1|+|a
1|≤M
1+|a
1|
同理：|b
n|≤M
2+|b
1|
记K
2=M
2+|b
2|，则有K
2=M
2+|b
2||a
n+1b
n+1-a
nb
n|=|a
n+1b
n+1-a
nb
n+1+a
nb
n+1-a
nb
n|≤|b
n+1||a
n+1-a
n|+|a
n||b
n+1-b
n|≤K
1|a
n+1-a
n|+k
1|b
n+1-b
n|
因此K
1（|b
n+1-b
n|+|b
n-b
n-1|+|a
2-a
1|）≤k
2M
1+k
1M
2+K
1（|b
n+1-b
n|+|b
n-b
n-1|+|a
2-a
1|）≤k
2M
1+k
1M
2故数列{a
nb
n}是B-数列．
点评：考查学生理解数列概念，灵活运用数列表示法的能力，旨在考查学生的观察分析和归纳能力，特别是问题（2）（3）的设置，增加了题目的难度，综合性较强，属难题．
阅读快车系列答案
，
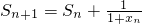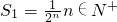
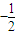的等比数列是否为B-数列？请说明理由；