
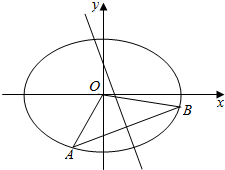
 已知椭圆$\frac{{x}^{2}}{2}$+y2=1上两个不同的点A,B关于直线$y=mx+\frac{1}{2}(m≠0)$对称.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1上两个不同的点A,B关于直线$y=mx+\frac{1}{2}(m≠0)$对称.分析 (1)设M(x,y),则$\frac{{x}^{2}}{2}$+y2=1,利用两点之间的距离公式、二次函数的单调性即可得出.
(2)由题意知m≠0,可设直线AB的方程为$y=-\frac{1}{m}x+b$.与椭圆方程联立得$\frac{{2+{m^2}}}{{2{m^2}}}{x^2}-\frac{2b}{m}x+{b^2}-1=0$.△>0,再利用中点坐标公式、根与系数的关系即可得出.
(3)利用弦长公式、点到直线的距离公式可得S△AOB,再利用二次函数的单调性即可得出.
解答 (1)证明:设M(x,y),则$\frac{{x}^{2}}{2}$+y2=1,
于是$|{MC}|=\sqrt{{x^2}+{{(y-\frac{1}{2})}^2}}$=$\sqrt{2-2{y^2}+{{(y-\frac{1}{2})}^2}}$=$\sqrt{-{y^2}-y+\frac{9}{4}}$=$\sqrt{-{{(y+\frac{1}{2})}^2}+\frac{5}{2}}$,
∵-1≤y≤1,
∴当$y=-\frac{1}{2}$时,${|{MC}|_{max}}=\frac{{\sqrt{10}}}{2}$.即$|{MC}|≤\frac{{\sqrt{10}}}{2}$.
(2)解:由题意知m≠0,可设直线AB的方程为$y=-\frac{1}{m}x+b$.
由$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\\ y=-\frac{1}{m}x+b\end{array}\right.$消去y,得$\frac{{2+{m^2}}}{{2{m^2}}}{x^2}-\frac{2b}{m}x+{b^2}-1=0$.
∵直线$y=-\frac{1}{m}x+b$与椭圆$\frac{x^2}{2}+{y^2}=1$有两个不同的交点,
∴$△=-2{b^2}+2+\frac{4}{m^2}>0$,
即${b^2}<1+\frac{2}{m^2}$ ①
将AB中点$M(\frac{2mb}{{{m^2}+2}},\frac{{{m^2}b}}{{{m^2}+2}})$,
代入直线方程$y=mx+\frac{1}{2}$解得$b=-\frac{{{m^2}+2}}{{2{m^2}}}$ ②
由①②得$m<-\frac{{\sqrt{6}}}{3}$或$m>\frac{{\sqrt{6}}}{3}$.
(3)解:令$t=\frac{1}{m}∈(-\frac{{\sqrt{6}}}{2},0)∪(0,\frac{{\sqrt{6}}}{2})$,即${t^2}=(0,\frac{3}{2})$,
则 $|{AB}|=\sqrt{{t^2}+1}•\frac{{\sqrt{-2{t^4}+2{t^2}+\frac{3}{2}}}}{{{t^2}+\frac{1}{2}}}$,
且O到直线AB的距离为$d=\frac{{{t^2}+\frac{1}{2}}}{{\sqrt{{t^2}+1}}}$,
设△AOB的面积为S(t),∴$S(t)=\frac{1}{2}|{AB}|•d=\frac{1}{2}\sqrt{-2{{({t^2}-\frac{1}{2})}^2}+2}≤\frac{{\sqrt{2}}}{2}$,
当且仅当${t^2}=\frac{1}{2}$时,等号成立.
故△AOB面积的最大值为$\frac{{\sqrt{2}}}{2}$.
点评 本题考查了椭圆的定义及其标准方程、直线与椭圆相交弦长问题、点到直线的距离公式、三角形面积计算公式、轴对称问题、两点之间的距离公式,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 4 | C. | -1或4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
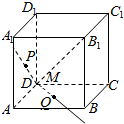 如图,M是正方体ABCD-A1B1C1D1对角线AC1上的动点,过点M作垂直于面ACC1A1的直线与正方体表面分别交于P、Q两点,设AM=x,PQ=y,则函数y=f(x)的图象大致为( )
如图,M是正方体ABCD-A1B1C1D1对角线AC1上的动点,过点M作垂直于面ACC1A1的直线与正方体表面分别交于P、Q两点,设AM=x,PQ=y,则函数y=f(x)的图象大致为( )| A. |  | B. | 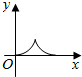 | C. | 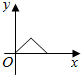 | D. | 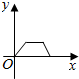 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
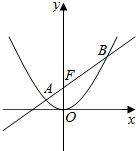 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com