
设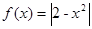 ,若
,若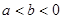 ,且
,且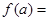
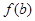 ,则
,则 的取值范围是
的取值范围是
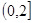
【解析】
试题分析:由于a,b小于0,所以只需研究x<0的函数的性质,利用绝对值的意义去掉绝对值符号,得到分段函数;当x<0时,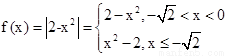 ,然后结合二次函数的
心智可知
,然后结合二次函数的
心智可知
∴f(x)在(-∞,-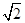 )递减;在(-
)递减;在(-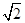 ,0)递增
,0)递增
∵a<b<0,且f(a)=f(b),代入解析式得到a,b的范围
∴a≤-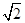 ,0>b>-
,0>b>-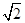 且a2-2=- a2+2,解得a=-
且a2-2=- a2+2,解得a=-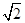 ;-
;-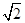 <b<0,∴0<ab<2
<b<0,∴0<ab<2
考点:本题考查利用绝对值的意义去掉绝对值符号,将绝对值函数转化为不含绝对值的函数、考查不等式的性质.
点评:解决该试题的关键是根据a,b小于0,所以只需研究x<0的函数的性质,利用绝对值的意义去掉绝对值符号,得到分段函数;得到f(x)在x<0上的单调性;判断出a,b的范围,利用f(a)=f(b),列出方程求出a的值,求出ab的范围.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com