
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{23}$ | B. | $\frac{{\sqrt{23}}}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
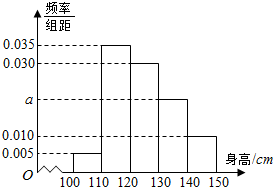 从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.
从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (0,2) | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
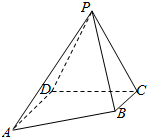 如图,四棱锥P-ABCD中,平面PCD⊥平面ABCD,△PCD是等边三角形,四边形ABCD是梯形,BC∥AD,BC⊥CD,AD=2BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,平面PCD⊥平面ABCD,△PCD是等边三角形,四边形ABCD是梯形,BC∥AD,BC⊥CD,AD=2BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com