不等式ax2-ax+4>0的解集为R,则a的取值范围是 ________
[0,16)
分析:分三种情况讨论:(1)当a等于0时,原不等式变为4大于0,显然成立;
(2)当a小于0时,根据二次函数的图象与性质可知解集为R不可能;
(3)当a大于0时,二次函数开口向上,且与x轴没有交点即△小于0时,函数值y恒大于0,即解集为R成立,根据△小于0列出不等式,求出a的范围,综上,得到满足题意的a的范围.
解答:(1)当a=0时,得到4>0,显然不等式的解集为R;
(2)当a>0时,二次函数y=ax
2-ax+4开口向上,由不等式的解集为R,得到二次函数与x轴没有交点即△=(-a)
2-16a<0,即a(a-16)<0,可化为
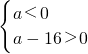
或
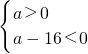
,解得0<a<16;
(3)当a<0时,二次函数y=ax
2-ax+4开口向下,函数值y不恒>0,故解集为R不可能.
综上,a的取值范围为[0,16)
故答案为:[0,16)
点评:本题考查一元二次不等式的解法,考查分类讨论及函数的思想,是中档题.

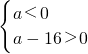 或
或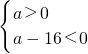 ,解得0<a<16;
,解得0<a<16;

 阅读快车系列答案
阅读快车系列答案