
(2)若x+3y-1=0,求证:2x+8y≥![]() .
.
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
已知a,b是正常数, a≠b, x,y![]() (0,+∞).
(0,+∞).
(1)求证:![]() ≥
≥![]() ,并指出等号成立的条件;w.w.w.k.s.5.u.c.o.m
,并指出等号成立的条件;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)利用(1)的结论求函数![]() 的最小值,并指出取最小值时相应的x 的值.
的最小值,并指出取最小值时相应的x 的值.
查看答案和解析>>
科目:高中数学 来源:2014届江西吉安二中高二月考文科数学试卷(解析版) 题型:选择题
已知a,b为正常数,F1,F2是两个定点,且|F1F2|=2a(a是正常数),动点P满足|PF1|+|PF2|=a2+1,则动点P的轨迹是( )
A.椭圆 B.线段 C.椭圆或线段 D.直线
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省高三上学期月考理科数学 题型:填空题
规定符号“ ”表示一种两个正实数之间的运算,即a
”表示一种两个正实数之间的运算,即a b=
b= ,a,b是正实
,a,b是正实
数,已知1 =3,则函数
=3,则函数 的值域是
.
的值域是
.
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省杭州外国语学校高二期中考试文科数学 题型:选择题
已知a,b,c是正实数,且a+b+c=1,则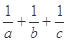 的最小值为( )
的最小值为( )
(A)3 (B) 6 (C) 9 (D) 12
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com