
 等边三角形的圆锥,过底面圆周上任一点作一平面α,且α与底面所成二面角为
等边三角形的圆锥,过底面圆周上任一点作一平面α,且α与底面所成二面角为 ,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
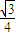



 ∠SEF得FH⊥SE,算出FH=6,即椭圆的长轴2a=6.利用△SBE的中位线和△OBF≌△OGH,算出BF=
∠SEF得FH⊥SE,算出FH=6,即椭圆的长轴2a=6.利用△SBE的中位线和△OBF≌△OGH,算出BF= EF=
EF= ,从而在底面圆中算出AB=
,从而在底面圆中算出AB=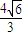 ,进而在△SAB中,利用平行线分线段成比例,得OC=
,进而在△SAB中,利用平行线分线段成比例,得OC= AB=
AB= ,即椭圆短半轴b=
,即椭圆短半轴b= .最后由椭圆的平方关系算出c=
.最后由椭圆的平方关系算出c= ,从而可得该椭圆的离心率.
,从而可得该椭圆的离心率. 设圆锥的顶点为S,轴截面为SEF,过F的一平面α与底面所成角为
设圆锥的顶点为S,轴截面为SEF,过F的一平面α与底面所成角为 ,α与母线SE交于点H,
,α与母线SE交于点H, =
= ∠SEF,得FH⊥SE
∠SEF,得FH⊥SE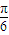 =4
=4 ×
× =6,即椭圆的长轴2a=6
=6,即椭圆的长轴2a=6
 BE
BE BE,可得BF=
BE,可得BF= EF=
EF=

 EF=
EF=
 =
= =
=

 ,可得OC=
,可得OC= AB=
AB= ,椭圆的短半轴b=
,椭圆的短半轴b=
 =
= ,椭圆的离心率e=
,椭圆的离心率e= =
=


科目:高中数学 来源: 题型:
 如图,轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.∠AOC=60°
如图,轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.∠AOC=60°查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•宜宾二模)如图,轴截面为边长为4
(2013•宜宾二模)如图,轴截面为边长为4| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川宜宾高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
如图,轴截面为边长为 等边三角形的圆锥,过底面圆周上任一点作一平面
等边三角形的圆锥,过底面圆周上任一点作一平面 ,且
,且 与底面所成二面角为
与底面所成二面角为 ,已知
,已知 与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )

A. B.
B. C.
C.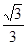 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014届山东冠县武训高中高二上学期10月月考文科数学试卷(解析版) 题型:解答题
(本题满分12分)
如图,轴截面为边长是2的正方形的圆柱 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆 的直径.
的直径.
(1)求三棱柱 的体积;
的体积;
(2)证明:平面 ⊥平面
⊥平面

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com