练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某校开设9门课程供学生选修，其中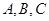三门由于上课时间相同，至多选一门，学校规定每位同学选修4门，共有　　 　　种不同选修方案。（用数值作答）

     

    【答案】

    75

    【解析】

    试题分析：解：∵A，B，C三门由于上课时间相同，至多选一门，第一类A，B，C三门课都不选，有C73=35种方案；，第二类A，B，C中选一门，剩余7门课中选两门，有C31C72=63种方案．，∴根据分类计数原理知共有35+63=98种方案．，故答案为75.

    考点：分类计数问题

    点评：本题考查分类计数问题，这是经常出现的一个问题，解题时一定要分清做这件事需要分为几类，每一类包含几种方法，把几个步骤中数字相加得到结果．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2007年普通高等学校招生全国统一考试、数学(江苏卷) 题型：022

    某校开设9门课程供学生选修，其中A，B，C三门由于上课时间相同，至多选一门，学校规定每位同学选修4门，共有________种不同选修方案．(用数值作答)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年内江市一模） 某校开设9门课程供学生选修，其中三门由于上课时间相同，至多选一门，学校规定，每位同学选修4门，共有__________种不同选修方案（用数值作答）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某校开设9门课程供学生选修，其中A、B、C三门由于上课时间相同，至多选一门，学校规定，每位同学选修4门，共有________________种不同的选修方案.（用数值作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    12.某校开设9门课程供学生选修，其中A、B、C三门由于上课时间相同，至多选一门，学校规定，每位同学选修4门，共有__________种不同的选修方案.（用数值作答）

    查看答案和解析>>

    同步练习册答案