
 相交于A、B两点,当t变化时,求|AB|的最大值.
相交于A、B两点,当t变化时,求|AB|的最大值. ,并整理得5x2+8tx+4t2-4=0①
,并整理得5x2+8tx+4t2-4=0①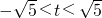 ,…(3分)
,…(3分) ,…(6分)
,…(6分)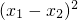 +
+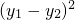 =2
=2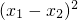 =2[
=2[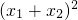 -4x1•x2]=2[
-4x1•x2]=2[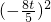
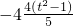 ]…(9分)
]…(9分) ,
,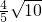 .…(12分)
.…(12分)

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
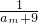 是数列{bn}的项;
是数列{bn}的项;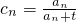 ,问:是否存在正整数t和k(k≥3),使得c1,c2,ck成等差数列?若存在,请求出所有符合条件的有序整数对(t,k);若不存在,请说明理由.
,问:是否存在正整数t和k(k≥3),使得c1,c2,ck成等差数列?若存在,请求出所有符合条件的有序整数对(t,k);若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 x+2ψ)(0<ψ<
x+2ψ)(0<ψ< )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com