
| 2 | 3 |
| 2 |
| 3 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| C | k 6 |
| 2 |
| 3 |
| 1 |
| 3 |
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||||
| P |
|
|
|
|
|
|
|
| 1 |
| 729 |
| 12 |
| 729 |
| 60 |
| 729 |
| 160 |
| 729 |
| 240 |
| 729 |
| 192 |
| 729 |
| 64 |
| 729 |
| 2916 |
| 729 |
| 2 |
| 3 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 32 |
| 81 |
| 32 |
| 81 |


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是![]() .
.
(1)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(2)求教师甲在一场比赛中获奖的概率;
(3)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
查看答案和解析>>
科目:高中数学 来源:2011届北京市朝阳区高三第一次综合练习数学理卷 题型:解答题
(本小题满分13分)
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是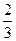 .
.
( Ⅰ)记教师甲在每场
Ⅰ)记教师甲在每场 的6次投球中投进球的个数为X,求X的分布列及数学期望;
的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比 赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省兖州市高三第三次模拟考试理科数学卷 题型:解答题
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是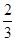 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com