
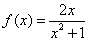 。
。科目:高中数学 来源:中学教材全解 高中数学 必修1(人教A版) 人教A版 题型:044
已知函数![]() .
.
(1)求图象的开口方向,对称轴,顶点坐标,与x轴交点坐标.
(2)求函数的单调区间,最值,零点.
(3)设图象与x轴相交于点(x1,0),(x2,0),不求出根,求|x1-x2|.
(4)已知![]() ,不计算函数值,求
,不计算函数值,求![]() .
.
(5)不计算函数值,试比较![]() 与
与![]() 的大小.
的大小.
(6)写出使函数值为负数的自变量x的集合.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北衡水中学高三上学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数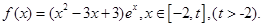
(1)当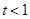 时,求函数
时,求函数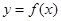 的单调区间;
的单调区间;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间。设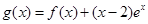 ,试问函数
,试问函数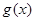 在
在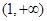 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省江门市开平市高一(上)期末数学试卷(解析版) 题型:解答题

 ,
, ,
, ,
, 这几个函数值,你能发现f(x)与
这几个函数值,你能发现f(x)与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;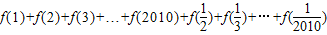 的值;
的值; 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com