
分析 求得f(x)的导数,设(x1,y1)为f(x)上的任一点,可得切线的斜率k1,求得g(x)的导数,设g(x)图象上一点(x2,y2)可得切线l2的斜率为k2,运用两直线垂直的条件:斜率之积为-1,分别求y=m-3cosx2的值域A,y=$\frac{1}{{e}^{{x}_{1}}+1}$值域B,由题意可得B⊆A,可得a的不等式,可得a的范围.
解答 解:f(x)=-ex-x的导数为f′(x)=-ex-1,
设(x1,y1)为f(x)上的任一点,
则过(x1,y1)处的切线l1的斜率为k1=-ex1-1,
g(x)=mx-3sinx的导数为g′(x)=m-3cosx,
过g(x)图象上一点(x2,y2)处的切线l2的斜率为k2=m-3cosx2.
由l1⊥l2,可得(-ex1-1)•(m-3cosx2)=-1,
即m-3cosx2=$\frac{1}{{e}^{{x}_{1}}+1}$,
任意的x1∈R,总存在x2∈R使等式成立.
则有y=m-3cosx2的值域为A=[m-3,m+3].
y=$\frac{1}{{e}^{{x}_{1}}+1}$的值域为B=(0,1),
有B⊆A,即(0,1)⊆[m-3,m+3].
即$\left\{\begin{array}{l}{m-3≤0}\\{m+3≥1}\end{array}\right.$,
解得-2≤a≤3.
故答案为:[-2,3].
点评 本题考查导数的运用:求切线的斜率,考查两直线垂直的条件:斜率之积为-1,考查任意存在性问题的解法,注意运用转化思想和值域的包含关系,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.
在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
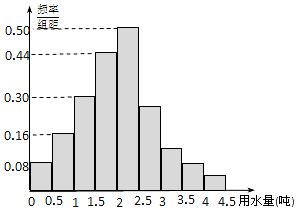 某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:| 分组 | 频数 |
| [0,0.5) | 4 |
| [0.5,1) | 8 |
| [1,1.5) | 15 |
| [1.5,2) | 22 |
| [2,2.5) | 25 |
| [2.5,3) | 14 |
| [3,3.5) | 6 |
| [3.5,4) | 4 |
| [4,4.5) | 2 |
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com