
(1) 在直角坐标系xOy中,曲线 的参数方程为
的参数方程为 为参数),M为
为参数),M为 上的动点,P点满足
上的动点,P点满足 ,点P的轨迹为曲线
,点P的轨迹为曲线 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线 与
与 的异于极点的交点为A,与
的异于极点的交点为A,与 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
(2) 某旅游景点给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、-2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内游戏庄家是赢是赔? 通过计算,你得到什么启示?
(1)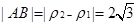 .
.
(2)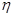 ~B(7,
~B(7,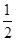 ). 一小时内有80人次玩.游戏庄家通常获纯利为(2+
). 一小时内有80人次玩.游戏庄家通常获纯利为(2+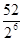 ×)80=225(元)
×)80=225(元)
答:庄家当然是赢家!我们应当学会以所学过的知识为武器,劝说人们不要被这类骗子的骗术所迷惑. 16分
【解析】
试题分析:设P(x,y),则由条件知M(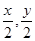 ).由于M点在C1上,所以
).由于M点在C1上,所以
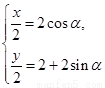 即
即 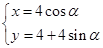
从而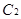 的参数方程为
的参数方程为 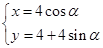 (
(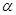 为参数) 4分
为参数) 4分
∴ 曲线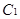 的极坐标方程为
的极坐标方程为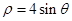 ,曲线
,曲线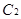 的极坐标方程为
的极坐标方程为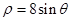 .
.
射线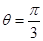 与
与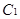 的交点
的交点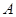 的极径为
的极径为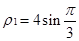 ,
,
射线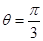 与
与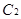 的交点
的交点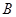 的极径为
的极径为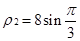 .
.
所以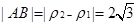 .
8分
.
8分
(2)

解:游人每玩一次,设游戏庄家获利为随机变量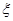 (元);游人每放一球,小球落入球槽,相当于做7次独立重复试验,设这个小球落入铁钉空隙从左到右的次序为随机变量+1,
(元);游人每放一球,小球落入球槽,相当于做7次独立重复试验,设这个小球落入铁钉空隙从左到右的次序为随机变量+1,
则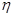 ~B(7,
~B(7,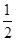 ). 10分
). 10分
因为P(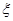 =-4)=P(
=-4)=P(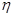 =0或
=0或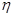 =7)=P(
=7)=P(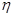 =0)+P(
=0)+P(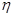 =7)=
=7)=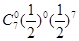 +
+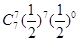 =
=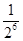
P(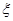 =-2)=P(
=-2)=P(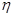 =1或
=1或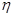 =6)=P(
=6)=P(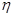 =1)+P(
=1)+P(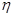 =6)=
=6)=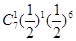 +
+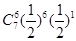 =
=
P(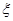 =0)=P(
=0)=P(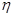 =2或
=2或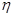 =5)=P(
=5)=P(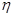 =2)+P(
=2)+P(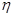 =5)=
=5)=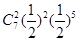 +
+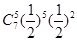 =
=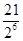
P(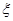 =2)=P(
=2)=P(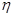 =3或
=3或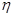 =4)=P(
=4)=P(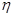 =3)+P(
=3)+P(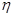 =4)=
=4)=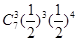 +
+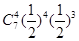 =
=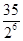
2+E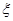 =2+(-4)×
=2+(-4)×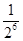 +(-2)×
+(-2)× +0×
+0×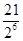 +2×
+2×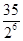 =2+
=2+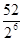 , 14分
, 14分
一小时内有80人次玩.游戏庄家通常获纯利为(2+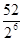 ×)80=225(元)
×)80=225(元)
答:庄家当然是赢家!我们应当学会以所学过的知识为武器,劝说人们不要被这类骗子的骗术所迷惑. 16分
考点:本题主要考查简单曲线的参数方程、极坐标方程,独立重复试验概率计算,随机变量的分布列及数学期望。
点评:综合题,本题综合考查简单曲线的参数方程、极坐标方程,独立重复试验概率计算,随机变量的分布列及数学期望。(2)作为应用问题,寓教于乐,令人生趣。对计算能力要求较高。


科目:高中数学 来源:新课标教材全解高中数学人教A版必修1 人教A版 题型:044
某公司今年一月份推出新产品A,成本为400元/件,经试销调查,销售量与销售价的关系如下表:
(1)在直角坐标系中,根据表中提供的数据描出实数对(x,y)的对应点,并确定x与y的一个函数关系式y=f(x);
(2)设经营此产品的月销售利润为S元,根据上述关系写出S关于x的函数关系,并指出当销售单价x为多少元时,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
(在下列两题中任选一题,若两题都做,按第1题给分)
1在直角坐标系中圆![]() 的参数方程为
的参数方程为
![]() (
(![]() 为参数),若以原点
为参数),若以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,则圆
轴正半轴为极轴建立极坐标系,则圆![]() 的极坐标方程为______ __.
的极坐标方程为______ __.
 2已知关于
2已知关于![]() 的不等式
的不等式![]() (
(![]() 是常数)的解是非空集合,则
是常数)的解是非空集合,则![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com