
(文)已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的标准方程;
(2)设直线
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,
,
(1)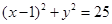 ;(2)
;(2)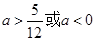 ;(3)
;(3)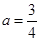
【解析】
试题分析:(1)由圆心在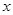 轴,可设圆心为
轴,可设圆心为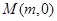 ,又直线
,又直线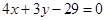 与圆相切,∴圆心到直线的距离
与圆相切,∴圆心到直线的距离 ,列式求
,列式求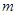 ,则圆的标准方程可求;(2)因为直线
,则圆的标准方程可求;(2)因为直线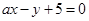
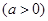 与圆相交于
与圆相交于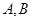 两点,则
两点,则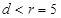 ,解不等式可求实数
,解不等式可求实数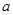 的取值范围;(3)首先根据垂直关系得
的取值范围;(3)首先根据垂直关系得 ,又直线
,又直线 过点
过点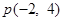 ,根据直线的点斜式方程写出
,根据直线的点斜式方程写出 的方程为
的方程为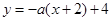 ,由垂径定理可知,弦
,由垂径定理可知,弦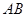 的垂直平分线必过圆心,将圆心
的垂直平分线必过圆心,将圆心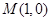 代入,可求
代入,可求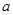 的值,再检验直线是否圆相交于两点.
的值,再检验直线是否圆相交于两点.
试题解析:(1)设圆心为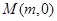 (m∈Z),由于圆与直线4x+3y-29=0相切,且半径为5,∴
(m∈Z),由于圆与直线4x+3y-29=0相切,且半径为5,∴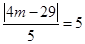 即|4m-29|=25,即4m-29=25或4m-29=-25,解得
即|4m-29|=25,即4m-29=25或4m-29=-25,解得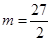 ,或
,或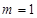 ,因为m为整数,故m=1,故所求的圆的方程是
,因为m为整数,故m=1,故所求的圆的方程是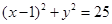 ;
;
(2) 此时,圆心C(1, 0)与该直线的距离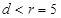 ,
,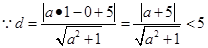
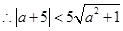
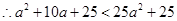 ,
,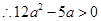 即:
即: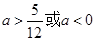 ;
;
(3)设符合条件的实数a存在,∵a≠0,则直线的 斜率为
斜率为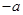 ,
, 的方程为
的方程为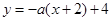 ,即
,即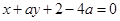 ,由于直线
,由于直线 垂直平分弦AB,故圆心M(1,0)必在
垂直平分弦AB,故圆心M(1,0)必在 ,所以1+0+2-4a=0,解得
,所以1+0+2-4a=0,解得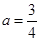 ,
,
经检验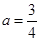 ,直线ax-y+5=0与圆有两个交点,故存在实数
,直线ax-y+5=0与圆有两个交点,故存在实数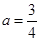 ,使得过点P(-2,4)的直线
,使得过点P(-2,4)的直线 垂直平分弦AB.
垂直平分弦AB.
考点:1、圆的标准方程;2、直线和圆的位置关系;3、点到直线的距离公式.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com